
分析 (1)求出圓的圓心C與半徑,利用圓心到直線l的距離,半徑半弦長滿足的勾股定理,求解弦長即可.
(2)將y=-ax-2a代入圓C的方程化簡,利用判別式為0,求出a,然后求解對稱圓的方程即可.
解答 (本小題滿分12分)
解:(1)∵圓C:${(x+2)^2}+{(y-2a)^2}={(\sqrt{3})^2}$,又$a=\frac{3}{2}$,
∴圓心C為(-2,3),直線l:3x+2y+6=0,…(1分)
圓心C到直線l的距離$d=\frac{|-6+6+6|}{{\sqrt{9+4}}}=\frac{{6\sqrt{13}}}{13}$,…(3分)
所以$AB=2\sqrt{3-\frac{36}{13}}=\frac{{2\sqrt{39}}}{13}$. …(5分)
(2)將y=-ax-2a代入圓C的方程化簡得:(1+a2)x2+4(1+2a2)x+16a2+1=0(*),
∴△=[4(1+2a2)]2-4(1+a2)(16a2+1)=4(3-a2)=0,
∵a>0,∴$a=\sqrt{3}$,…(7分)
∴方程(*)的解$x=-\frac{7}{2}$,∴切點坐標為($-\frac{7}{2}$,$\frac{{3\sqrt{3}}}{2}$),…(9分)
根據圓關于切線對稱的性質可知切點為CC′的中點,故圓C′的坐標
為(-5,$\sqrt{3}$),…(11分)
∴圓C'的方程為:${(x+5)^2}+{(y-\sqrt{3})^2}=3$. …(12分)
點評 本題考查直線與圓的方程的應用,考查轉化思想以及計算能力.


 七星圖書口算速算天天練系列答案
七星圖書口算速算天天練系列答案 初中學業考試導與練系列答案
初中學業考試導與練系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
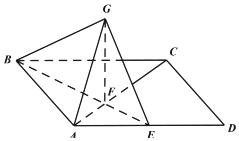 如圖,四邊形 ABCD是平行四邊形,AB=1,AD=2,AC=$\sqrt{3}$,E 是 AD的中點,BE與AC 交于點F,GF⊥平面ABCD.
如圖,四邊形 ABCD是平行四邊形,AB=1,AD=2,AC=$\sqrt{3}$,E 是 AD的中點,BE與AC 交于點F,GF⊥平面ABCD.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | y=x-1 | B. | $y={({\frac{1}{2}})^x}$ | C. | $y=\frac{1}{1-x}$ | D. | y=x2-4x |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | n2 | B. | n(n+1) | C. | $\frac{n(n+1)}{2}$ | D. | (n+1)(n+2) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com