
 如圖,在三棱柱ABC-A1B1C1中,A1A⊥平面ABC,∠BAC=90°,F為棱AA1上的動點,A1A=4,AB=AC=2.
如圖,在三棱柱ABC-A1B1C1中,A1A⊥平面ABC,∠BAC=90°,F為棱AA1上的動點,A1A=4,AB=AC=2.分析 (1)以點A為原點建立空間直角坐標系,求出相關點的坐標,平面BFC1的一個法向量,利用向量的數量積求解直線BC與平面BFC1所成角的正弦值.
(2)設$F(0,0,t)(0≤t≤4),\overrightarrow{BF}=(-2,0,t),\overrightarrow{B{C_1}}=(-2,2,4)$,求出平面BFC1的一個法向量,平面FC1C的一個法向量,利用向量的數量積求解二面角B-FC1-C的大小.
解答 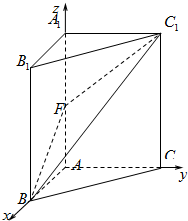 (本題滿分16分)
(本題滿分16分)
解:如圖,以點A為原點建立空間直角坐標系,依題意得A(0,0,0),B(2,0,0),C(0,2,0),A1(0,0,4),C1(0,2,4),
(1)因為F為中點,則$F(0,0,2),\overrightarrow{BF}=(-2,0,2),\overrightarrow{B{C_1}}=(-2,2,4),\overrightarrow{BC}=(-2,2,0)$,
設$\overrightarrow n=(x,y,z)$是平面BFC1的一個法向量,
則$\left\{\begin{array}{l}\overrightarrow n•\overrightarrow{BF}=-2x+2z=0\\ \overrightarrow n•\overrightarrow{B{C_1}}=-2x+2y+4z=0\end{array}\right.$,取x=1,則$\overrightarrow n=(1,-1,1)$,…(4分)
則$cos\left?{\overrightarrow{BC}•\overrightarrow n}\right>=\frac{{\overrightarrow{BC}•\overrightarrow n}}{{|\overrightarrow{BC}|•|\overrightarrow n|}}=\frac{-4}{{2\sqrt{2}•\sqrt{3}}}=-\frac{{\sqrt{6}}}{3}$,…(6分)
所以直線BC與平面BFC1所成角的正弦值為$\frac{{\sqrt{6}}}{3}$
所以直線BC與平面BFC1所成角的余弦值為$\sqrt{1-{{({\frac{{\sqrt{6}}}{3}})}^2}}=\frac{{\sqrt{3}}}{3}$…(8分)
(2)設$F(0,0,t)(0≤t≤4),\overrightarrow{BF}=(-2,0,t),\overrightarrow{B{C_1}}=(-2,2,4)$,
設$\overrightarrow n=(x,y,z)$是平面BFC1的一個法向量,
則$\left\{\begin{array}{l}\overrightarrow n•\overrightarrow{BF}=-2x+tz=0\\ \overrightarrow n•\overrightarrow{B{C_1}}=-2x+2y+4z=0\end{array}\right.$,取z=2,則$\overrightarrow n=(t,t-4,2)$…(11分
)$\overrightarrow{AB}=(2,0,0)$是平面FC1C的一個法向量,
則$cos<\overrightarrow n,\overrightarrow{AB}>=\frac{{\overrightarrow n•\overrightarrow{AB}}}{{|\overrightarrow n|•|\overrightarrow{AB}|}}=\frac{2t}{{2\sqrt{{t^2}+{{(t-4)}^2}+4}}}$,…(14分)
∴$|{\frac{2t}{{2\sqrt{{t^2}+{{(t-4)}^2}+4}}}}|=\frac{{\sqrt{2}}}{2}$,得$t=\frac{5}{2}$,即$AF=\frac{5}{2},F{A_1}=\frac{3}{2}$,
所以當$\frac{AF}{{F{A_1}}}=\frac{5}{3}$時,二面角B-FC1-C的大小是45°. …(16分)
點評 本題考查二面角的平面角的求法,直線與平面所成角的求法,考查空間想象能力以及計算能力.


 智慧課堂密卷100分單元過關檢測系列答案
智慧課堂密卷100分單元過關檢測系列答案 單元期中期末卷系列答案
單元期中期末卷系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 色盲 | 不色盲 | 合計 | |
| 男 | 38 | 442 | 480 |
| 女 | 6 | 514 | 520 |
| 合計 | 44 | 956 | 1000 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 3≤a<5 | B. | 0<a<4 | C. | 4<a<5或0≤a≤3 | D. | 3<a<5或0≤a<3 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com