
分析 如果“(¬p)∧q”為真,則p假,q真,進而得到實數a的取值范圍.
解答 解:若函數f(x)=x3-ax-1在區間[-1,1]上單調遞增;
則數f′(x)=3x2-a≥0在區間[-1,1]上恒成立,
即a≤3x2在區間[-1,1]上恒成立,
解得:a≤0,
故命題p:a≤0,
若函數y=ln(ax2+x+1)的值域是R.
則a=0,或$\left\{\begin{array}{l}a>0\\△=1-4a≥0\end{array}\right.$,
解得:0≤a≤$\frac{1}{4}$,
即命題q:0≤a≤$\frac{1}{4}$,
如果“(¬p)∧q”為真,
則p假,q真,
故0<a≤$\frac{1}{4}$
點評 本題以命題的真假判斷與應用為載體,考查了復合命題,利用導數研究函數的單調性,函數恒成立問題等知識點,難度中檔.


科目:高中數學 來源: 題型:選擇題
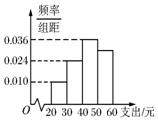 學校為了調查學生在課外讀物方面的支出情況,抽取了一個容量為n的樣本,其頻率分布直方圖如圖,其中支出在[50,60)的同學有30人,若想在這n人中抽取50人,則在[50,60)之間應抽取的人數為( )
學校為了調查學生在課外讀物方面的支出情況,抽取了一個容量為n的樣本,其頻率分布直方圖如圖,其中支出在[50,60)的同學有30人,若想在這n人中抽取50人,則在[50,60)之間應抽取的人數為( )| A. | 10人 | B. | 15人 | C. | 25人 | D. | 30人 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
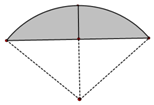 《九章算術》是我國古代數學成就的杰出代表.其中《方田》章給出計算弧田面積所用的經驗公式為:弧田面積=$\frac{1}{2}$(弦×矢+矢2).弧田由圓弧和其所對弦所圍成,公式中“弦”指圓弧所對弦長,“矢”等于半徑長與圓心到弦的距離之差.按照上述經驗公式計算所得弧田面積與其實際面積之間存在誤差.
《九章算術》是我國古代數學成就的杰出代表.其中《方田》章給出計算弧田面積所用的經驗公式為:弧田面積=$\frac{1}{2}$(弦×矢+矢2).弧田由圓弧和其所對弦所圍成,公式中“弦”指圓弧所對弦長,“矢”等于半徑長與圓心到弦的距離之差.按照上述經驗公式計算所得弧田面積與其實際面積之間存在誤差.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 年齡(歲) | 頻率 | |
| 第1組 | [25,30) | 0.1 |
| 第2組 | [30,35) | 0.1 |
| 第3組 | [35,40) | 0.4 |
| 第4組 | [40,45) | 0.3 |
| 第5組 | [45,50] | 0.1 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (0,+∞) | B. | (0,$\frac{3}{2}$) | C. | (-1,3) | D. | ($-\frac{1}{2}$,$\frac{3}{2}$) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com