(本題滿分10分)已知數列
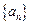
的前
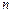
項和為
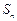
,通項公式為

,
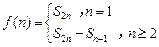
.(Ⅰ)計算
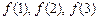
的值;(Ⅱ)比較
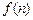
與1的大小,并用數學歸納法證明你的結論.
(Ⅰ)由已知
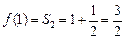
,
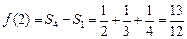
,
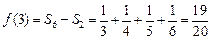
;……3分
(Ⅱ)由(Ⅰ)知
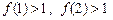
;當
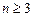
時,猜想:
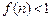
.…4分
下面用數學歸納法證明:
(1)由(Ⅰ)當
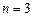
時,
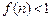
; ……5分
(2)假設
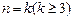
時,
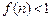
,即
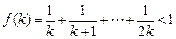
,那么
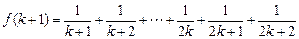
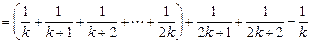
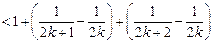
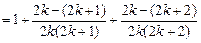
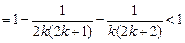
,所以當
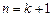
時,
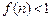
也成立. 由(1)和(2)知,當
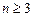
時,
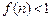
.……9分
所以當
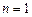
,和
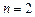
時,
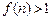
;當
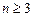
時,
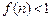
. …10分
練習冊系列答案
相關習題
科目:高中數學
來源:不詳
題型:單選題
設數列
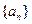
的前
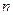
項和為
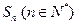
,關于數列
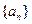
有下列三個命題:
①若數列
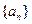
既是等差數列又是等比數列,則
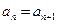
;
②若
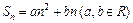
,則數列
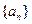
是等差數列;
③若
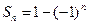
,則數列
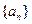
是等比數列.
這些命題中,真命題的個數是
.
查看答案和解析>>
科目:高中數學
來源:不詳
題型:解答題
(12分)數列{a
n}滿足a
1=1,a
2=2,a
n+2=(1+cos
2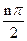
)a
n+sin
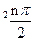
,n=1、2、3…1)求a
3、a
4并求數列{a
n}的通項公式(2)設b
n=
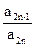
,令 S
n=
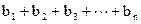
求S
n
查看答案和解析>>
科目:高中數學
來源:不詳
題型:解答題
設
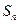
為數列
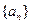
的前
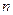
項和,
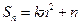
,
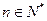
,其中
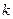
是常數.
(I)求
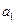
及
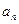
;
(II)若對于任意的
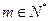
,
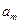
,

,
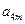
成等比數列,求
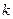
的值.
查看答案和解析>>
科目:高中數學
來源:不詳
題型:解答題
(本小題滿分12分)
已知不等式
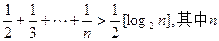
為大于2的整數,
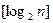
表示不超過
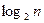
的最大整數. 設數列
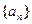
的各項為正,且滿足
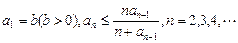
(Ⅰ)證明
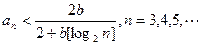
(Ⅱ)猜測數列
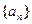
是否有極限?如果有,寫出極限的值(不必證明);
(Ⅲ)試確定一個正整數N,使得當
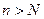
時,對任意
b>0,都有
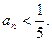
.
查看答案和解析>>
科目:高中數學
來源:不詳
題型:解答題
(理)過點P(1,0)作曲線
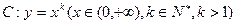
的切線,切點為M
1,設M
1在x軸上的投影是點P
1.又過點P
1作曲線C的切線,切點為M
2,設M
2在x軸上的投影是點P
2,….依此下去,得到一系列點M
1,M
2…,M
n,…,設它們的橫坐標a
1,a
2,…,a
n,…,構成數列為
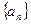
.
(1)求證數列
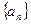
是等比數列,并求其通項公式;
(2)求證:
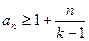
;(3)當
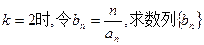
的前n項和S
n.
查看答案和解析>>
科目:高中數學
來源:不詳
題型:解答題
(本小題滿分12分)等差數列
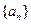
的前
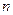
項和為
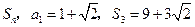
.
⑴求數列
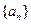
的通項
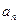
與前
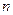
項和
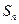
;⑵設
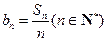
,求證:數列
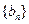
中任意不同的三項都不可能成為等比數列.
查看答案和解析>>
科目:高中數學
來源:不詳
題型:填空題
等差數列{
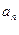
}前n項和為
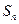
。已知
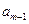
+
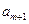
-
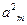
=0,
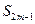
=38,則m=_______
查看答案和解析>>
主站蜘蛛池模板:
在线观看理论电影
|
欧美一区二区三区成人
|
日本免费电影一区
|
国产激情视频在线观看
|
成人99
|
久久久网
|
精品视频 免费
|
国产中文在线播放
|
欧美视频一区
|
午夜精品久久久久久久久久久久久
|
国产视频一区在线
|
欧美久久久久久
|
欧美淫片
|
欧美精品成人一区二区三区四区
|
色偷偷噜噜噜亚洲男人
|
国产四区
|
蜜臀久久99精品久久久久久宅男
|
日本啪啪网站
|
自拍视频在线观看
|
国产精品久久久久久久久久
|
伊人伊人|
日本特级片
|
一区二区三区在线观看视频
|
亚洲国产一区二区三区四区
|
亚洲第一国产精品
|
狠狠av|
日韩免费在线视频
|
日本视频在线观看
|
国产精品99久久久久久宅男
|
伊人超碰
|
三级av
|
久久久久网站
|
污网站在线观看视频
|
国产精品久久免费视频
|
国产视频一区二区
|
亚洲精品乱码久久久久久蜜桃不卡
|
欧美日一区二区
|
亚洲国产91
|
成人在线播放
|
三级av|
欧美激情欧美激情在线五月
|

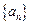 的前
的前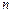 項和為
項和為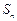 ,通項公式為
,通項公式為 ,
,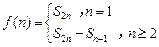 .(Ⅰ)計算
.(Ⅰ)計算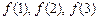 的值;(Ⅱ)比較
的值;(Ⅱ)比較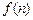 與1的大小,并用數學歸納法證明你的結論.
與1的大小,并用數學歸納法證明你的結論. 寒假大串聯黃山書社系列答案
寒假大串聯黃山書社系列答案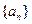 的前
的前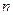 項和為
項和為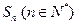 ,關于數列
,關于數列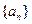 有下列三個命題:
有下列三個命題: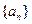 既是等差數列又是等比數列,則
既是等差數列又是等比數列,則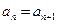 ;
;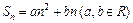 ,則數列
,則數列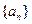 是等差數列;
是等差數列;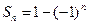 ,則數列
,則數列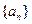 是等比數列.
是等比數列.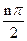 )an+sin
)an+sin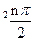 ,n=1、2、3…1)求a3、a4并求數列{an}的通項公式(2)設bn=
,n=1、2、3…1)求a3、a4并求數列{an}的通項公式(2)設bn=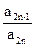 ,令 Sn=
,令 Sn=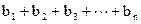 求Sn
求Sn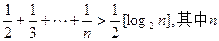 為大于2的整數,
為大于2的整數,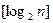 表示不超過
表示不超過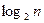 的最大整數. 設數列
的最大整數. 設數列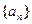 的各項為正,且滿足
的各項為正,且滿足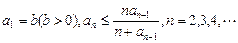
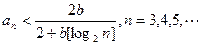
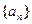 是否有極限?如果有,寫出極限的值(不必證明);
是否有極限?如果有,寫出極限的值(不必證明);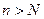 時,對任意b>0,都有
時,對任意b>0,都有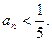 .
.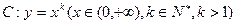 的切線,切點為M1,設M1在x軸上的投影是點P1.又過點P1作曲線C的切線,切點為M2,設M2在x軸上的投影是點P2,….依此下去,得到一系列點M1,M2…,Mn,…,設它們的橫坐標a1,a2,…,an,…,構成數列為
的切線,切點為M1,設M1在x軸上的投影是點P1.又過點P1作曲線C的切線,切點為M2,設M2在x軸上的投影是點P2,….依此下去,得到一系列點M1,M2…,Mn,…,設它們的橫坐標a1,a2,…,an,…,構成數列為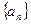 .
.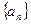 是等比數列,并求其通項公式;
是等比數列,并求其通項公式;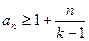 ;(3)當
;(3)當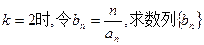 的前n項和Sn.
的前n項和Sn.