
【題目】已知橢圓![]()
![]() 經過點
經過點![]() ,
,![]() ,過點
,過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于不同的兩點
交于不同的兩點![]()
![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)求![]() 的取值范圍;
的取值范圍;
(3)設直線![]() 和直線
和直線![]() 的斜率分別為
的斜率分別為![]() 和
和![]() ,求證:
,求證:![]() 為定值.
為定值.
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】如圖所示,太極圖是由黑白兩個魚形紋組成的圖案,俗稱陰陽魚.太極圖展現了一種相互轉化,相對統一的和諧美.定義:能夠將圓![]() 的周長和面積同時等分成兩個部分的函數稱為圓
的周長和面積同時等分成兩個部分的函數稱為圓![]() 的一個“太極函數”.現有下列說法:①對于圓
的一個“太極函數”.現有下列說法:①對于圓![]() :
:![]() 的所有非常數函數的太極函數中,一定不能為偶函數;②函數
的所有非常數函數的太極函數中,一定不能為偶函數;②函數![]() 是圓
是圓![]() :
:![]() 的一個太極函數;③存在圓
的一個太極函數;③存在圓![]() ,使得
,使得![]() 是圓
是圓![]() 的一個太極函數;④直線
的一個太極函數;④直線![]() 所對應的函數一定是圓
所對應的函數一定是圓![]() :
:![]() (
(![]() )的太極函數;⑤若函數
)的太極函數;⑤若函數![]() (
(![]() )是圓
)是圓![]() :
:![]() 的太極函數,則
的太極函數,則![]() .其中正確的是__________.
.其中正確的是__________.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 在橢圓
在橢圓![]() 上,過點
上,過點![]() 作
作![]() 軸于點
軸于點![]()
(1)求線段![]() 的中點的軌跡
的中點的軌跡![]() 的方程
的方程
(2)設![]() 、
、![]() 兩點在(1)中軌跡
兩點在(1)中軌跡![]() 上,點
上,點![]() ,兩直線
,兩直線![]() 與
與![]() 的斜率之積為
的斜率之積為![]() ,且(1)中軌跡
,且(1)中軌跡![]() 上存在點
上存在點![]() 滿足
滿足![]() ,當
,當![]() 面積最小時,求直線
面積最小時,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于數列![]() ,定義“
,定義“![]() 變換”:
變換”:![]() 將數列
將數列![]() 變換成數列
變換成數列![]() ,其中
,其中![]() ,且
,且![]() ,這種“
,這種“![]() 變換”記作
變換”記作![]() .繼續對數列
.繼續對數列![]() 進行“
進行“![]() 變換”,得到數列
變換”,得到數列![]() ,依此類推,當得到的數列各項均為
,依此類推,當得到的數列各項均為![]() 時變換結束.
時變換結束.
(1)試問![]() 和
和![]() 經過不斷的“
經過不斷的“![]() 變換”能否結束?若能,請依次寫出經過“
變換”能否結束?若能,請依次寫出經過“![]() 變換”得到的各數列;若不能,說明理由;
變換”得到的各數列;若不能,說明理由;
(2)求![]() 經過有限次“
經過有限次“![]() 變換”后能夠結束的充要條件;
變換”后能夠結束的充要條件;
(3)證明:![]() 一定能經過有限次“
一定能經過有限次“![]() 變換”后結束.
變換”后結束.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,矩形ABCD中,![]() ,
,![]() ,點F、E分別是BC、CD的中點,現沿AE將
,點F、E分別是BC、CD的中點,現沿AE將![]() 折起,使點D至點M的位置,且
折起,使點D至點M的位置,且![]() .
.


(1)證明:![]() 平面MEF;
平面MEF;
(2)求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某房地產公司新建小區有A、B兩種戶型住宅,其中A戶型住宅每套面積為100平方米,B戶型住宅每套面積為80平方米,該公司準備從兩種戶型住宅中各拿出12套銷售給內部員工,表是這24套住宅每平方米的銷售價格:(單位:萬元平方米):
房號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
A戶型 | 2.6 | 2.7 | 2.8 | 2.8 | 2.9 | 3.2 | 2.9 | 3.1 | 3.4 | 3.3 | 3.4 | 3.5 |
B戶型 | 3.6 | 3.7 | 3.7 | 3.9 | 3.8 | 3.9 | 4.2 | 4.1 | 4.1 | 4.2 | 4.3 | 4.5 |
(1)根據表格數據,完成下列莖葉圖,并分別求出A,B兩類戶型住宅每平方米銷售價格的中位數;
A戶型 | B戶型 | |
2. | ||
3. | ||
4. |
(2)該公司決定對上述24套住房通過抽簽方式銷售,購房者根據自己的需求只能在其中一種戶型中通過抽簽方式隨機獲取房號,每位購房者只有一次抽簽機會,小明是第一位抽簽的員工,經測算其購買能力最多為320萬元,抽簽后所抽得住房價格在其購買能力范圍內則確定購買,否則,將放棄此次購房資格,為了使其購房成功的概率更大,他應該選擇哪一種戶型抽簽?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知F1,F2為橢圓E:![]() 的左、右焦點,且|F1F2|=2
的左、右焦點,且|F1F2|=2![]() ,點
,點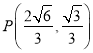 在E上.
在E上.
(1)求E的方程;
(2)直線l與以E的短軸為直徑的圓相切,l與E交于A,B兩點,O為坐標原點,試判斷O與以AB為直徑的圓的位置關系,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com