
已知集合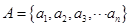 ,
,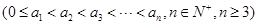
具有性質 :對任意的
:對任意的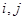
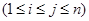 ,
,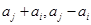 至少有一個屬于
至少有一個屬于 .
.
(1)分別判斷集合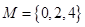 與
與 是否具有性質
是否具有性質 ;
;
(2)求證:①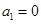 ;
;
②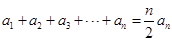 ;
;
(3)當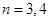 或
或 時集合
時集合 中的數列
中的數列 是否一定成等差數列?說明理由.
是否一定成等差數列?說明理由.
(1) 有 ,
有 , 沒有;(2)證明見解析;(3)
沒有;(2)證明見解析;(3)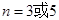 時,是等差數列,
時,是等差數列, 時,不一定.
時,不一定.
解析試題分析:(1)對于具體的集合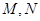 ,我們根據定義直接驗證即可,如集合
,我們根據定義直接驗證即可,如集合 ,
,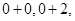
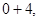
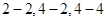 均屬于集合
均屬于集合 ,故
,故 個有性質
個有性質 ,而集合
,而集合 ,
,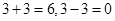 均不屬于
均不屬于 ,則
,則 不具有性質
不具有性質 ;(2)
;(2)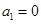 易證,等式
易證,等式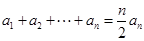 變形得
變形得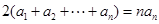 ,聯想到等差數列的前
,聯想到等差數列的前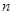 項和求法,是不是有
項和求法,是不是有 (這是成立的),
(這是成立的),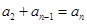 (?),
(?), (?),…,由于
(?),…,由于 ,故
,故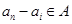 ,從而可看出只能是
,從而可看出只能是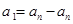 ,
,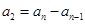 ,
,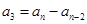 ,…,
,…,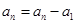 ,即
,即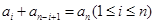 成立,②式得證;(3)如果答案是肯定的,必須證明,如果答案是不確定的,則要舉例說明,
成立,②式得證;(3)如果答案是肯定的,必須證明,如果答案是不確定的,則要舉例說明, 時,集合
時,集合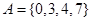 具有性質
具有性質 ,但不是等差數列,
,但不是等差數列,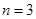 和
和 時,具有性質
時,具有性質 的集合
的集合 中的數列是等差數列,
中的數列是等差數列,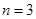 時易證,首先
時易證,首先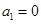 ,然后
,然后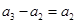 ,即
,即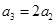 ,故
,故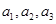 成等差,
成等差,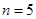 時,難一點,由(2)知
時,難一點,由(2)知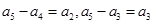 ,兩式相減可得
,兩式相減可得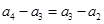 ,而由于
,而由于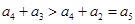 ,即
,即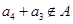 ,則有
,則有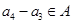 ,注意到
,注意到 ,于是
,于是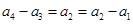 ,又有
,又有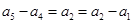 ,故數列
,故數列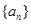 是等差數列,
是等差數列,
試題解析:(1)∵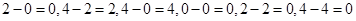 ≒∴集合
≒∴集合 具有性質
具有性質 ,
,
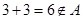 ,
,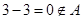 ,
, 集合
集合 不具有性質
不具有性質 . 3分
. 3分
(2)由已知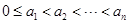 ,
,
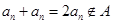 ,
,
則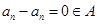 ,仍由
,仍由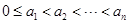 知
知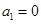 ; 5分
; 5分
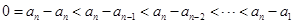

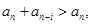


 天天練口算系列答案
天天練口算系列答案科目:高中數學 來源: 題型:解答題
(12分)(2011•湖北)成等差數列的三個正數的和等于15,并且這三個數分別加上2、5、13后成為等比數列{bn}中的b3、b4、b5.
(Ⅰ)求數列{bn}的通項公式;
(Ⅱ)數列{bn}的前n項和為Sn,求證:數列{Sn+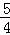 }是等比數列.
}是等比數列.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(2013•浙江)在公差為d的等差數列{an}中,已知a1=10,且a1,2a2+2,5a3成等比數列.
(1)求d,an;
(2)若d<0,求|a1|+|a2|+|a3|+…+|an|.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
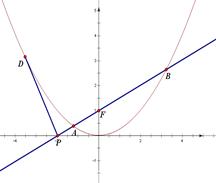
拋物線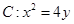 ,直線
,直線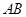 過拋物線
過拋物線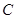 的焦點
的焦點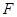 ,交
,交 軸于點
軸于點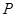 .
.
(1)求證: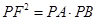 ;
;
(2)過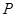 作拋物線
作拋物線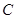 的切線,切點為
的切線,切點為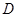 (異于原點),
(異于原點),
(ⅰ)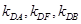 是否恒成等差數列,請說明理由;
是否恒成等差數列,請說明理由;
(ⅱ)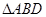 重心的軌跡是什么圖形,請說明理由.
重心的軌跡是什么圖形,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
下列命題正確的是 ( )
①若數列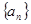 是等差數列,且
是等差數列,且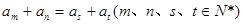 ,
,
則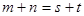 ;
;
②若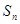 是等差數列
是等差數列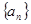 的前
的前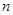 項的和,則
項的和,則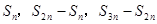 成等差數列;
成等差數列;
③若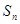 是等比數列
是等比數列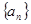 的前
的前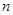 項的和,則
項的和,則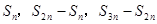 成等比數列;
成等比數列;
④若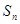 是等比數列
是等比數列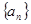 的前
的前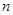 項的和,且
項的和,且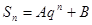 ;(其中
;(其中 是非零常數,
是非零常數,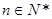 ),則
),則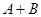 為零.
為零.
| A.①② | B.②③ | C.②④ | D.③④ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com