
分析 求出函數的導數,解關于導函數的不等式,求出函數的單調區間,從而求出函數的極值即可.
解答 解:函數的定義域D=(-∞,+∞),且在(-∞,+∞)上,
y′=$\frac{(1+x)(1-x)}{{{(x}^{2}+1)}^{2}}$,
令 y′=0,得 x=1或 x=-1,
在(-∞,-1)內,y′<0;在(-1,1)內,y′>0;
在(1,+∞)內,y′<0,
∴函數在(-∞,-1)遞減,在(-1,1)遞增,在(1,+∞)遞減,
∴x=-1時,函數有極小值,極小值是-$\frac{1}{2}$,
x=1時,函數有極大值,極大值是$\frac{1}{2}$,
函數無最大值和最小值.
點評 本題考查了函數的單調性、極值問題,考查導數的應用,是一道基礎題.


 小學生10分鐘口算測試100分系列答案
小學生10分鐘口算測試100分系列答案科目:高中數學 來源: 題型:選擇題
| A. | “a<b”是“am2<bm2”的充要條件 | |
| B. | 命題“?x∈R,x3-x2-1≤0”的否定是“?x∈R,x3-x2-1≤0” | |
| C. | “若 a,b都是奇數,則 a+b是偶數”的逆否命題是“若 a+b不是偶數,則 a,b不都是奇數” | |
| D. | 若 p∧q為假命題,則 p,q均為假命題 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | M∩N=M | B. | M∪(∁UN)=U | C. | M∩(∁UN)=∅ | D. | M⊆∁UN |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (1)(3)(4) | B. | (1)(2)(3) | C. | (3)(4) | D. | (4) |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
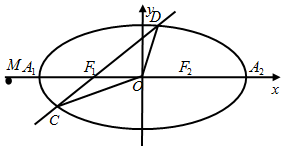 (文科)如圖,已知橢圓的中心在坐標原點,焦點F1,F2,在x軸上,長軸A1A2的長為4,x軸上一點M(${-\frac{a^2}{c},0}$),$|{\overrightarrow{M{A_1}}}|$=$2|{\overrightarrow{{A_1}{F_1}}}|$.
(文科)如圖,已知橢圓的中心在坐標原點,焦點F1,F2,在x軸上,長軸A1A2的長為4,x軸上一點M(${-\frac{a^2}{c},0}$),$|{\overrightarrow{M{A_1}}}|$=$2|{\overrightarrow{{A_1}{F_1}}}|$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com