Question

20．設(shè)$f（x）=sin\frac{1}{2}πx，g（x）=\frac{1}{6}（x-2）$，則方程f（x）=g（x）的所有解的和為10．

Answer 1

分析 f（x）的周期是T=4，且關(guān)于點（2，0）對稱； 函數(shù)g（x）=$\frac{1}{6}$（x-2）過點（2，0）且斜率為k=$\frac{1}{6}$，作圖發(fā)現(xiàn)，g（x）過點（8，0）、（-4，0），根據(jù)圖形，f（x）=g（x）的有5個根，且一個根是x=2；其余的4個根關(guān)于2對稱，即可得出結(jié)論．

解答 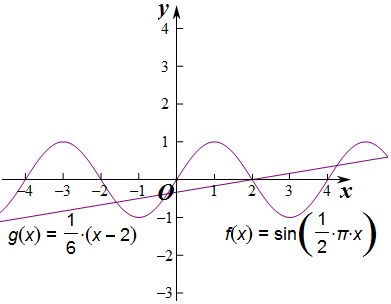解：f（x）的周期是T=4，
且關(guān)于點（2，0）對稱；
函數(shù)g（x）=$\frac{1}{6}$（x-2）
過點（2，0）且斜率為k=$\frac{1}{6}$，
作圖發(fā)現(xiàn)，g（x）過點（8，0）、（-4，0），根據(jù)圖形，
f（x）=g（x）的有5個根，
且一個根是x=2；
其余的4個根關(guān)于2對稱，
則所有根的和是10．
故答案為10．

點評 本題考查方程解的問題，考查數(shù)形結(jié)合的數(shù)學(xué)思想，考查學(xué)生分析解決問題的能力，正確作出函數(shù)的圖象是關(guān)鍵．