
分析 (Ⅰ)設直線l:x=my+n,代入拋物線方程,由韋達定理y1y2=-2pn,代入${x_1}{x_2}=\frac{{{{({y_1}{y_2})}^2}}}{{4{p^2}}}={n^2}$,由$\overrightarrow{OA}=({x_1},{y_1})$,$\overrightarrow{OB}=({x_2},{y_2})$,由$\overrightarrow{OA}•\overrightarrow{OB}=0$,x1x2+y1y2=0,即可得到n=2p,代入x=my+2p,因此直線l過定點(2p,0);
(Ⅱ)p=2時,求得直線l的方程,代入拋物線方程,由韋達定理求得y1+y2=4m,y1y2=-16,由弦長公式可得:丨AB丨=$\sqrt{1+{m}^{2}}$•丨y1-y2丨=$\sqrt{1+{m}^{2}}$•$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=4$\sqrt{{m}^{4}+5{m}^{2}+4}$,由函數的單調性可知:m=0時,|AB|min=8.
解答 解:(Ⅰ)證明:設直線l:x=my+n,
∴$\left\{\begin{array}{l}{x=my+n}\\{{y}^{2}=2px}\end{array}\right.$,可得y2-2pmy-2pn=0,
∴△=4p2m2+8pn>0,
由韋達定理可得:y1y2=-2pn,
∴${x_1}{x_2}=\frac{{{{({y_1}{y_2})}^2}}}{{4{p^2}}}={n^2}$,
又$\overrightarrow{OA}=({x_1},{y_1})$,$\overrightarrow{OB}=({x_2},{y_2})$
∴OA⊥OB,
∴$\overrightarrow{OA}•\overrightarrow{OB}=0$,即x1x2+y1y2=0,
∴n2-2pn=0,
又∵n≠0,
∴n=2p,
∴x=my+2p,
直線l過定點(2p,0),滿足△>0;
(Ⅱ)p=2時,y2=4x,
由$\left\{\begin{array}{l}{x=mx+4}\\{{y}^{2}=4x}\end{array}\right.$,整理可得:y2-4my-16=0,
y1+y2=4m,y1y2=-16,
則$\begin{array}{l}|AB|=\sqrt{1+{m^2}}|{y_1}-{y_2}|=\sqrt{1+{m^2}}\sqrt{{{({y_1}+{y_2})}^2}-4{y_1}{y_2}}\\=\sqrt{1+{m^2}}•\sqrt{16{m^2}+64}=4\sqrt{(1+{m^2})({m^2}+4)}=4\sqrt{{m^4}+5{m^2}+4}\end{array}$,
∵m4≥0,m2≥0,
∴m=0時,|AB|min=8.
點評 本題考查直線與拋物線的位置關系,考查韋達定理,向量數量積的坐標表示,向量垂直的充要條件及弦長公式,考查計算能力,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | 1,-1 | B. | -1 | C. | 1 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 30° | B. | 60° | C. | 90° | D. | 不確定 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
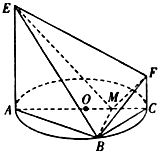 如圖,AC是圓O的直徑,點 B在圓 O上,∠B AC=30°,B M⊥AC交 AC于點 M,E A⊥平面 A BC,FC∥E A,AC=4,E A=3,FC=1.
如圖,AC是圓O的直徑,點 B在圓 O上,∠B AC=30°,B M⊥AC交 AC于點 M,E A⊥平面 A BC,FC∥E A,AC=4,E A=3,FC=1.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (0,$\frac{1}{36}$] | B. | (0,$\frac{1}{9}$] | C. | (0,$\frac{1}{6}$] | D. | (0,$\frac{1}{3}$] |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com