
| A. | 4π | B. | 8π | C. | 12π | D. | 16π |
分析 根據題意,將四面體ABCD放置于如圖所示的正方體中,則正方體的外接球就是四面體ABCD的外接球.因此利用題中數據算出外接球半徑R,當球心O到截面的距離最大時,截面圓的面積達最小值,再利用球的截面圓性質可算出截面面積的最小值.
解答 解:將四面體ABCD放置于正方體中,如圖所示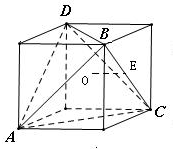
可得正方體的外接球就是四面體ABCD的外接球,
∵正四面體ABCD的棱長為4,∴正方體的棱長為2$\sqrt{2}$,
可得外接球半徑R滿足2R=2$\sqrt{2}$×$\sqrt{3}$,R=$\sqrt{6}$.
E為棱BC的中點,過E作其外接球的截面,當球心O到截面的距離最大時,截面圓的面積達最小值,
此時球心O到截面的距離等于正方體棱長的一半,可得截面圓的半徑為r=$\sqrt{{R}^{2}-2}=2$.
得到截面圓的面積最小值為S=πr2=4π.
故選:A.
點評 本題給出正四面體的外接球,求截面圓的面積最小值.著重考查了正方體的性質、球內接多面體和球的截面圓性質等知識,屬于中檔題.


 優等生題庫系列答案
優等生題庫系列答案 53天天練系列答案
53天天練系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| 男 | 女 | 總計 | |
| 喜歡 | 40 | 20 | 60 |
| 不喜歡 | 20 | 30 | 50 |
| 總計 | 60 | 50 | 110 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| A. | 在犯錯誤的概率不超過0.1%的前提下,認為“喜歡該節目與性別有關” | |
| B. | 在犯錯誤的概率不超過0.1%的前提下,認為“喜歡該節目與性別無關” | |
| C. | 有99%以上的把握認為“喜歡該節目與性別有關” | |
| D. | 有99%以上的把握認為“喜歡該節目與性別無關” |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{6}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
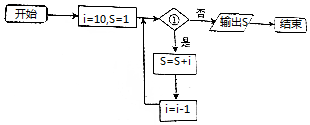
| A. | (5,6] | B. | [5,6) | C. | (6,7] | D. | [6,7) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com