
分析 (Ⅰ)令h(x)=f(x)-1+$\frac{1}{x}$=lnx-1+$\frac{1}{x}$,(x>0).確定函數h(x)單調性及最值即可.
(Ⅱ)g(x)=x2f(x)=x2lnx,(x>0)
(i)g′(x)=x(2lnx+1),確定g(x)的單調性,畫出g(x)的圖象,即可求出實數m的取值范圍.
(ii)由(i)方程f(x)=m(m<-2)的兩個相異實根x1,x2,滿足 0<x1<$\frac{1}{\sqrt{e}}$<x2<1,
令F(x)=x2lnx-m,則有F(x1)═f(x2)
構造函數G(x)=F(x)-F($\frac{{e}^{-\frac{e}{2}}}{{x}^{2}}$)=x2lnx-$\frac{{e}^{-e}}{{x}^{4}}(-\frac{e}{2}-2lnx)$,($\frac{1}{\sqrt{e}}$<x<1),
利用導數得F(x1)=F(x2)$>F(\frac{{e}^{-\frac{e}{2}}}{{{x}_{2}}^{2}})$,且x1,$\frac{{e}^{-\frac{e}{2}}}{{{x}_{2}}^{2}}$∈(0,$\frac{1}{\sqrt{e}}$),即可證明x1x22<${e}^{-\frac{e}{2}}$.
解答 解:(1)證明:令h(x)=f(x)-1+$\frac{1}{x}$=lnx-1+$\frac{1}{x}$,(x>0).
h′(x)=$\frac{1}{x}-\frac{1}{{x}^{2}}$=$\frac{x-1}{{x}^{2}}$,
x∈(0,1)時,h′(x)<0,x∈(1,+∞),h′(x)>0,
h(x)在(0,1)遞減,在(1,+∞)遞增,
h(x)≥h(1)=0,即f(x)≥1-$\frac{1}{x}$成立;
(Ⅱ)g(x)=x2f(x)=x2lnx,(x>0)
(i)g′(x)=x(2lnx+1),令g′(x)=0,得x=$\frac{1}{\sqrt{e}}$.
x$∈(0,\frac{1}{\sqrt{e}}$)時,g′(x)<0,x$∈(\frac{1}{\sqrt{e}},+∞)$時,g′(x)>0,
∴g(x)在(0,$\frac{1}{\sqrt{e}}$)遞減,在($\frac{1}{\sqrt{e}},+∞)$遞增,
g(x)min=g($\frac{1}{\sqrt{e}}$)=-$\frac{1}{2e}$,且x→0,時g(x)→0,g(1)=0.
g(x)的圖象如下:
要使關于x的方程x2f(x)=m有兩個不等的實根x1,x2(x1<x2).
實數m的取值范圍為:(-$\frac{1}{2e}$,0).
(ii)證明:由(i)方程f(x)=m(m<-2)的兩個相異實根x1,x2,滿足 0<x1<$\frac{1}{\sqrt{e}}$<x2<1,
令F(x)=x2lnx-m,則有F(x1)═f(x2)
構造函數G(x)=F(x)-F($\frac{{e}^{-\frac{e}{2}}}{{x}^{2}}$)=x2lnx-$\frac{{e}^{-e}}{{x}^{4}}(-\frac{e}{2}-2lnx)$,($\frac{1}{\sqrt{e}}$<x<1),
G′(x)>0,且G($\frac{1}{\sqrt{e}}$)>0,
∴$F(x)>F(\frac{{e}^{-\frac{e}{2}}}{{x}^{2}})$在$\frac{1}{\sqrt{e}}$<x<1時恒成立,
則有F(x1)=F(x2)$>F(\frac{{e}^{-\frac{e}{2}}}{{{x}_{2}}^{2}})$,且x1,$\frac{{e}^{-\frac{e}{2}}}{{{x}_{2}}^{2}}$∈(0,$\frac{1}{\sqrt{e}}$)
由(i)知F(x)在(0,$\frac{1}{\sqrt{e}}$)遞減,∴${x}_{1}<\frac{{e}^{-\frac{e}{2}}}{{{x}_{2}}^{2}}$,
∴x1x22<${e}^{-\frac{e}{2}}$.
點評 本題考查導數知識的運用,考查函數的單調性,考查不等式的證明、運算能力,正確構造函數是關鍵.屬于難題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 3 | 7 | 5 | 9 | 6 | 1 | 8 | 2 | 4 |
| A. | 7560 | B. | 7564 | C. | 7550 | D. | 7554 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [5,+∞) | B. | (5,+∞) | C. | (-∞,5] | D. | (-∞,5) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f(x)>0恒成立 | B. | f(x)<0 | ||
| C. | 當且僅當x∈(-∞,1),f(x)<0 | D. | 當且僅當x∈(1,+∞),f(x)>0 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {x|0≤x≤4} | B. | {x|-1≤x≤4} | C. | {x|-1≤x≤0} | D. | {x|0<x≤4} |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
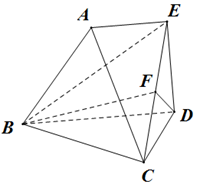 如圖所示,在多面體ABCDE中,△BCD是邊長為2的正三角形,AE∥DB,AE⊥DE,2AE=BD,DE=1,面ABDE⊥面BCD,F是CE的中點.
如圖所示,在多面體ABCDE中,△BCD是邊長為2的正三角形,AE∥DB,AE⊥DE,2AE=BD,DE=1,面ABDE⊥面BCD,F是CE的中點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com