
| A. | $\frac{19}{10}$ | B. | $\frac{29}{20}$ | C. | $\frac{40}{21}$ | D. | $\frac{36}{19}$ |
分析 當n≥2時,$\frac{{a}_{n}}{{2}^{n}}$=$\frac{{a}_{n-1}}{{2}^{n-1}}$+n-1,即有$\frac{{a}_{n}}{{2}^{n}}-\frac{{a}_{n-1}}{{2}^{n-1}}=n+1$
可得($\frac{{a}_{2}}{{2}^{2}}-\frac{{a}_{1}}{{2}_{1}})+(\frac{{a}_{3}}{{2}^{3}}-\frac{{a}_{2}}{{2}^{2}})+…(\frac{{a}_{n}}{{2}^{2}}-\frac{{a}_{n-1}}{{2}^{n-1}})$+($\frac{{a}_{3}}{{2}^{3}}-\frac{{a}_{2}}{{2}^{2}}$)+…+($\frac{{a}_{n}}{{2}^{n}}-\frac{{a}_{n-1}}{{2}^{n-1}}$)=1+2+…+(n-1)
bn=$\frac{{a}_{n}}{{2}^{n}}$-1=$\frac{n(n-1)}{2}$,$\frac{1}{{b}_{n}}$=2($\frac{1}{n-1}-\frac{1}{n}$)
則$\frac{1}{{b}_{2}}$+$\frac{1}{{b}_{3}}$+…+$\frac{1}{{b}_{20}}$+…+$\frac{1}{{b}_{n}}$=2($\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}$+…+$\frac{1}{n-1}-\frac{1}{n}$)即可求解
解答 解:∵當n≥2時,$\frac{{a}_{n}}{{2}^{n}}$=$\frac{{a}_{n-1}}{{2}^{n-1}}$+n-1,∴$\frac{{a}_{n}}{{2}^{n}}-\frac{{a}_{n-1}}{{2}^{n-1}}=n+1$
$\frac{{a}_{2}}{{2}^{2}}-\frac{{a}_{1}}{{2}^{1}}=1,\frac{{a}_{3}}{{2}^{3}}-\frac{{a}_{2}}{{2}^{2}}=2,…\frac{{a}_{n}}{{2}^{n}}-\frac{{a}_{n-1}}{{2}^{n-1}}=n-1$
∴($\frac{{a}_{2}}{{2}^{2}}-\frac{{a}_{1}}{{2}_{1}})+(\frac{{a}_{3}}{{2}^{3}}-\frac{{a}_{2}}{{2}^{2}})+…(\frac{{a}_{n}}{{2}^{2}}-\frac{{a}_{n-1}}{{2}^{n-1}})$+($\frac{{a}_{3}}{{2}^{3}}-\frac{{a}_{2}}{{2}^{2}}$)+…+($\frac{{a}_{n}}{{2}^{n}}-\frac{{a}_{n-1}}{{2}^{n-1}}$)=1+2+…+(n-1)
∴$\frac{{a}_{n}}{{2}^{n}}-\frac{{a}_{1}}{{2}^{1}}=\frac{(n-1)(1+n-1)}{2}=\frac{n(n-1)}{2}$
∴bn=$\frac{{a}_{n}}{{2}^{n}}$-1=$\frac{n(n-1)}{2}$,$\frac{1}{{b}_{n}}$=2($\frac{1}{n-1}-\frac{1}{n}$)
∴則$\frac{1}{{b}_{2}}$+$\frac{1}{{b}_{3}}$+…+$\frac{1}{{b}_{20}}$+…+$\frac{1}{{b}_{n}}$=2($\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}$+…+$\frac{1}{n-1}-\frac{1}{n}$)
故$\frac{1}{{b}_{2}}$+$\frac{1}{{b}_{3}}$+…+$\frac{1}{{b}_{20}}$等于2(1-$\frac{1}{20}$)=$\frac{19}{10}$
故選:A
點評 本題考查了累加法求數列通項,裂項相消法求和,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | 1+$\sqrt{6}$ | B. | 1+$\sqrt{5}$ | C. | 1+$\sqrt{3}$ | D. | 1+$\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
 將一張邊長為12cm的正方形紙片按如圖(1)所示陰影部分裁去四個全等的等腰三角形,將余下部分沿虛線折疊并拼成一個有底的正四棱錐模型,如圖(2)所示放置.如果正四棱錐的主視圖是等邊三角形,如圖(3)所示,則正四棱錐的體積是( )
將一張邊長為12cm的正方形紙片按如圖(1)所示陰影部分裁去四個全等的等腰三角形,將余下部分沿虛線折疊并拼成一個有底的正四棱錐模型,如圖(2)所示放置.如果正四棱錐的主視圖是等邊三角形,如圖(3)所示,則正四棱錐的體積是( )| A. | $\frac{32}{3}$$\sqrt{6}$cm3 | B. | $\frac{64}{3}$$\sqrt{6}$cm3 | C. | $\frac{32}{3}$$\sqrt{2}$cm3 | D. | $\frac{64}{3}$$\sqrt{2}$cm3 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
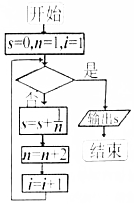
| A. | i>1010 | B. | i<1010 | C. | i>1009 | D. | i<1009 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 5$\sqrt{13}$ | B. | 5$\sqrt{11}$ | C. | 5$\sqrt{7}$ | D. | 5 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 恰有1名女生與恰有2名女生 | B. | 至少有1名男生與全是男生 | ||
| C. | 至少有1名男生與至少有1名女生 | D. | 至少有1名女生與全是男生 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{4}{5}$ | B. | $\frac{6}{5}$ | C. | $\frac{8}{5}$ | D. | 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com