Question

5．已知函數f（x）=$\sqrt{3}$sinxcosx的圖象與函數g（x）=3sin²x-λ（λ∈R）的圖象在$[{-\frac{π}{4}，\frac{π}{2}}]$上有兩個交點，則實數λ的取值范圍是（　　）

• A． $（\frac{{3-2\sqrt{3}}}{2}，0]$
• B． $（\frac{{3-2\sqrt{3}}}{2}，3]$
• C． $（\frac{{3-2\sqrt{3}}}{2}，\frac{{3+2\sqrt{3}}}{2}]$
• D． $（\frac{{3-2\sqrt{3}}}{2}，\frac{{3+2\sqrt{3}}}{2}]$

Answer 1

分析 由題意，令函數F（x）=f（x）-g（x），f（x）和g（x）交點問題轉化為F（x）的零點問題，又令F（x）=0轉化為三角函數圖象與直線的交點問題，在$[{-\frac{π}{4}，\frac{π}{2}}]$上求出三角函數的值域，利用圖象可得解．

解答 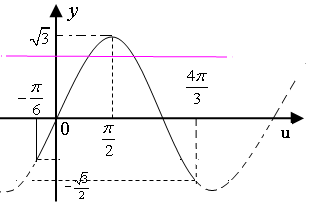解：由題意，令函數F（x）=f（x）-g（x），
即F（x）=$\sqrt{3}$sinxcosx-3sin²x+λ=$\frac{\sqrt{3}}{2}$sin2x+$\frac{3}{2}$cos2x+λ$-\frac{3}{2}$=$\sqrt{3}$sin（2x+$\frac{π}{3}$）+λ$-\frac{3}{2}$．
要求F（x）的零點，令F（x）=0，可得$\sqrt{3}$sin（2x+$\frac{π}{3}$）+λ$-\frac{3}{2}$=0．
轉化為函數y=$\sqrt{3}$sin（2x+$\frac{π}{3}$）與y=$\frac{3}{2}-λ$圖象的交點問題．
當x在$[{-\frac{π}{4}，\frac{π}{2}}]$上時，
令2x+$\frac{π}{3}$=u，
則：u∈[$-\frac{π}{6}$，$\frac{4π}{3}$]．
可得y=$\sqrt{3}$sinu的圖象如下：
從圖象看出：$-\frac{1}{2}×\sqrt{3}$≤$\frac{3}{2}-λ$$＜\sqrt{3}$時，圖象由兩個交點，
∴$-\frac{2+\sqrt{3}}{2}≤$-λ＜$\frac{2\sqrt{3}-3}{2}$．
故選：C．

點評 本題考查了三角函數交點的問題，轉化為令函數零點的問題，構造成新函數，利用圖象求解，屬于中檔題．