【題目】已知函數
.
(Ⅰ)求函數
的最小值；
(Ⅱ)解不等式
【答案】（1）5；（2）
.
【解析】試題分析：⑴利用絕對值不等式的性質，求得函數的最小值；
⑵方法一：去掉絕對值，寫成分段函數的形式，然后求解；方法二：作出函數的圖象，數形結合，解不等式
解析：(Ⅰ)因為f(x)＝|2x－1|＋2|x＋2|≥|(2x－1)－2(x＋2)|＝5，
所以
(Ⅱ)解法一：f(x)＝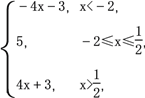
當x<－2時，由－4x－3<8，解得x>－
，即－<x<－2；
當－2≤x≤
時，5<8恒成立，即－2≤x≤；
當x>時，由4x＋3<8，解得x<
，即<x<，
所以原不等式的解集為
.
解法二(圖象法)：f(x)＝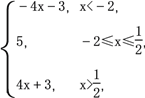
函數f(x)的圖象如圖所示，
令f(x)＝8，解得x＝－或x＝，
所以不等式f(x)<8的解集為.
科目：高中數學 來源： 題型：
【題目】已知函數
（
是自然對數的底數）
（1）若直線
為曲線
的一條切線，求實數
的值；
（2）若函數
在區間
上為單調函數，求實數
的取值范圍；
（3）設
，若
在定義域上有極值點（極值點是指函數取得極值時對應的自變量的值），求實數
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的離心率
，左、右焦點分別為
，且
與拋物線
的焦點重合.
（1）求橢圓的標準方程；
（2）若過
的直線交橢圓于
兩點，過
的直線交橢圓于
兩點，且
，求
的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】隨著科學技術的飛速發展，手機的功能逐漸強大，很大程度上代替了電腦、電視.為了了解某高校學生平均每天使用手機的時間是否與性別有關，某調查小組隨機抽取了
名男生、
名女生進行為期一周的跟蹤調查，調查結果如表所示:
平均每天使用手機超過 | 平均每天使用手機不超過 | 合計 | |
男生 |
|
|
|
女生 |
|
|
|
合計 |
|
|
|
（1）能否在犯錯誤的概率不超過
的前提下認為學生使用手機的時間長短與性別有關？
（2）在這
名女生中，調查小組發現共有
人使用國產手機，在這
人中，平均每天使用手機不超過
小時的共有
人.從平均每天使用手機超過
小時的女生中任意選取
人，求這
人中使用非國產手機的人數
的分布列和數學期望.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
參考公式：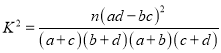 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，曲線
的參數方程是
(
為參數)，以原點
為極點， 
軸正半軸為極軸，建立極坐標系，直線
的極坐標方程為
.
(Ⅰ)求曲線
的普通方程與直線
的直角坐標方程；
(Ⅱ)已知直線
與曲線
交于
， 
兩點，與
軸交于點
，求
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
