Question

8．已知正n棱錐的體積V為定值，試確定其側面與底面所成的二面角的大小，使得正n棱錐的表面積取得最小值．

Answer 1

分析 設其側面與底面所成的二面角的大小為α，以正四棱錐為例，設正四棱錐的底面正方形的邊長為2a，高為h，建立關系，利用基本不等式求解表面積最小時的體積與邊長的關系，從而確定其側面與底面所成的二面角的大小．

解答 解：設其側面與底面所成的二面角的大小為α，以正四棱錐為例，體積V為定值，設正四棱錐的底面正方形的邊長為2a，高為h，
則側面的高為h′=$\sqrt{{h}^{2}+{a}^{2}}$，
棱錐的體積V=$\frac{1}{3}$Sh=$\frac{1}{3}$4a²h，則${a}^{2}=\frac{3v}{4h}$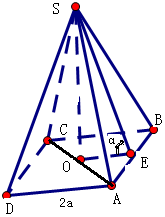
表面積S=4×$\frac{1}{2}$×h′×2a=4a×h′=4a$\sqrt{{h}^{2}+{a}^{2}}$=4×$\sqrt{\frac{3V}{4h}×（{h}^{2}-\frac{3V}{4h}）}$=4×$\sqrt{\frac{3Vh}{4}+\frac{9{V}^{2}}{16{h}^{2}}}$
∵$\frac{3Vh}{8}+\frac{3Vh}{8}+\frac{9{V}^{2}}{16{h}^{2}}$≥3×$\root{3}{\frac{3V×3V×9{V}^{2}}{64×16}}$=$\frac{9V}{4}\root{3}{\frac{3V}{16}}$，
（當且僅當$\frac{3Vh}{8}=\frac{9{V}^{2}}{16{h}^{2}}$時，即h=$\root{3}{\frac{3V}{2}}$取等號）．
而此時側面與底面所成的二面角α，有$tanα=\frac{h}{a}$，
可得：$tanα=\frac{4（\frac{3}{2}V）^{\frac{2}{3}}}{3V}$
故得：側面與底面所成的二面角α=arctan（$\frac{4（\frac{3}{2}V）^{\frac{2}{3}}}{3V}$）．

點評 本題考察了正n棱錐的體積V與底面積，表面積之間的關系，基本不等式求解表面積最小時的體積與邊長的關系，從而確定其側面與底面所成的二面角的大小是解題的關鍵．屬于中檔題．