
分析 (1)利用指數的運算性質即可得出.
(2)利用對數的運算性質即可得出.
解答 解:(Ⅰ)原式=$(\frac{3}{2})^{3×(-\frac{2}{3})}$+$50{0}^{-1×(-\frac{1}{2})}$-$\frac{10(\sqrt{5}+2)}{(\sqrt{5}-2)(\sqrt{5}+2)}$+1=$\frac{4}{9}$+10$\sqrt{5}$-10$\sqrt{5}$-20+1=-$\frac{167}{9}$
(Ⅱ)原式=$lg\frac{\frac{4\sqrt{2}}{7}×\sqrt{245}}{{2}^{2}}$=lg$\sqrt{10}$=$\frac{1}{2}$.
點評 本題考查了指數與對數的運算性質,考查了推理能力與計算能力,屬于基礎題.


 名師點撥卷系列答案
名師點撥卷系列答案 英才計劃期末調研系列答案
英才計劃期末調研系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
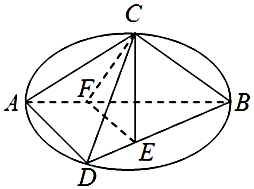 如圖C,D是以AB為直徑的圓上的兩點,AB=2AD=2$\sqrt{3}$,AC=BC,F是AB上的一點,且AF=$\frac{1}{3}$AB,CE⊥面ABD,CE=$\sqrt{2}$.
如圖C,D是以AB為直徑的圓上的兩點,AB=2AD=2$\sqrt{3}$,AC=BC,F是AB上的一點,且AF=$\frac{1}{3}$AB,CE⊥面ABD,CE=$\sqrt{2}$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $a≥\frac{1}{8}$ | B. | $0<a≤\frac{1}{16}$ | C. | $-\frac{1}{8}≤a<0$ | D. | $-\frac{1}{2}<a≤\frac{1}{16}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0 | B. | 1 | C. | 2 | D. | e+1 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | y=2-|x| | B. | y=tanx | C. | y=-x3 | D. | $y={log_{\frac{1}{5}}}x$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com