
【題目】教材曾有介紹:圓![]() 上的點
上的點![]() 處的切線方程為
處的切線方程為![]() 。我們將其結論推廣:橢圓
。我們將其結論推廣:橢圓![]() 上的點
上的點![]() 處的切線方程為
處的切線方程為![]() ,在解本題時可以直接應用。已知,直線
,在解本題時可以直接應用。已知,直線![]() 與橢圓
與橢圓![]() 有且只有一個公共點.
有且只有一個公共點.
(1)求![]() 的值;
的值;
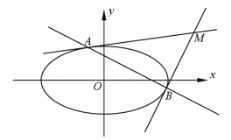
(2)設![]() 為坐標原點,過橢圓
為坐標原點,過橢圓![]() 上的兩點
上的兩點![]() 、
、![]() 分別作該橢圓的兩條切線
分別作該橢圓的兩條切線![]() 、
、![]() ,且
,且![]() 與
與![]() 交于點
交于點![]() 。當
。當![]() 變化時,求
變化時,求![]() 面積的最大值;
面積的最大值;
(3)在(2)的條件下,經過點![]() 作直線
作直線![]() 與該橢圓
與該橢圓![]() 交于
交于![]() 、
、![]() 兩點,在線段
兩點,在線段![]() 上存在點
上存在點![]() ,使
,使![]() 成立,試問:點
成立,試問:點![]() 是否在直線
是否在直線![]() 上,請說明理由.
上,請說明理由.
【答案】(1)![]() (2)
(2)![]() (3)見解析
(3)見解析
【解析】
(1)將直線y=x![]() 代入橢圓方程,得到x的方程,由直線和橢圓相切的條件:判別式為0,解方程可得a的值;(2)設切點A(x1,y1),B(x2,y2),可得切線
代入橢圓方程,得到x的方程,由直線和橢圓相切的條件:判別式為0,解方程可得a的值;(2)設切點A(x1,y1),B(x2,y2),可得切線![]() ,
,![]() ,
,![]() ,再將M代入上式,結合兩點確定一條直線,可得切點弦方程,AB的方程為x+my=1,將直線與橢圓方程聯立,運用韋達定理,求得△OAB的面積,化簡整理,運用基本不等式即可得到所求最大值;(3)點
,再將M代入上式,結合兩點確定一條直線,可得切點弦方程,AB的方程為x+my=1,將直線與橢圓方程聯立,運用韋達定理,求得△OAB的面積,化簡整理,運用基本不等式即可得到所求最大值;(3)點![]() 在直線
在直線![]() 上,因為
上,因為![]()
設![]() 、
、![]() 、
、![]() ,且
,且![]() ,于是
,于是![]() ,向量坐標化,得
,向量坐標化,得![]() 、
、![]() 、
、![]() 、
、![]() ,將
,將![]() 代入橢圓方程,結合
代入橢圓方程,結合![]() 、
、![]() 在橢圓上,整理化簡得
在橢圓上,整理化簡得![]() ,即
,即![]() 在直線
在直線![]() 上.
上.
(1)聯立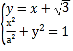 ,整理得
,整理得![]()
依題意![]() ,即
,即![]()
(2)設![]() 、
、![]() ,于是直線
,于是直線![]() 、
、![]() 的方程分別為
的方程分別為![]() 、
、![]()
將![]() 代入
代入![]() 、
、![]() 的方程得
的方程得![]() 且
且![]()
所以直線![]() 的方程為
的方程為![]()
聯立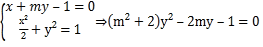
顯然![]() ,由
,由![]() ,
,![]() 是該方程的兩個實根,有
是該方程的兩個實根,有![]() ,
,![]()
![]() 面積
面積![]()
即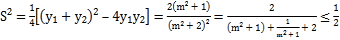
當且僅當![]() 時,“=”成立,
時,“=”成立,![]() 取得最大值
取得最大值![]()
(3)點![]() 在直線
在直線![]() 上,因為
上,因為![]()
設![]() 、
、![]() 、
、![]() ,且
,且![]()
于是![]() ,即
,即![]() 、
、![]() 、
、![]() 、
、![]()
又![]() ,
,![]()
![]() ,
,
![]() ,即
,即![]() 在直線
在直線![]() 上.
上.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,動點
中,動點![]() 到定點
到定點![]() 的距離與
的距離與![]() 到定直線
到定直線![]() 的距離的比為
的距離的比為![]() ,動點
,動點![]() 的軌跡記為
的軌跡記為![]() .
.
(1)求軌跡![]() 的方程;
的方程;
(2)若點![]() 在軌跡
在軌跡![]() 上運動,點
上運動,點![]() 在圓
在圓![]() 上運動,且總有
上運動,且總有![]() ,
,
求![]() 的取值范圍;
的取值范圍;
(3)過點![]() 的動直線
的動直線![]() 交軌跡
交軌跡![]() 于
于![]() 兩點,試問:在此坐標平面上是否存在一個定點
兩點,試問:在此坐標平面上是否存在一個定點![]() ,使得無論
,使得無論![]() 如何轉動,以
如何轉動,以![]() 為直徑的圓恒過點
為直徑的圓恒過點![]() ?若存在,求出點
?若存在,求出點![]() 的坐標.若不存在,請說明理由.
的坐標.若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公交公司為了方便市民出行,科學規劃車輛投放,在一個人員密集流動地段增設一個起點站,為了研究車輛發車間隔時間x與乘客等候人數y之間的關系,經過調查得到如下數據:
間隔時間x/分 | 10 | 11 | 12 | 13 | 14 | 15 |
等候人數y/人 | 23 | 25 | 26 | 29 | 28 | 31 |
調查小組先從這6組數據中選取4組數據求線性回歸方程,再用剩下的2組數據進行檢驗.檢驗方法如下:先用求得的線性回歸方程計算間隔時間對應的等候人數![]() ,再求
,再求![]() 與實際等候人數y的差,若差值的絕對值都不超過1,則稱所求方程是“恰當回歸方程”.
與實際等候人數y的差,若差值的絕對值都不超過1,則稱所求方程是“恰當回歸方程”.
(1)從這6組數據中隨機選取4組數據,求剩下的2組數據的間隔時間相鄰的概率;
(2)若選取的是中間4組數據,求y關于x的線性回歸方程![]() ,并判斷此方程是否是“恰當回歸方程”.
,并判斷此方程是否是“恰當回歸方程”.
附:對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: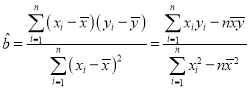 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓![]() :
: ![]() 的離心率為
的離心率為![]() ,短軸端點與兩焦點圍成的三角形面積為
,短軸端點與兩焦點圍成的三角形面積為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,且過點
兩點,且過點![]() ,
,![]() 為坐標原點,當△
為坐標原點,當△![]() 為直角三角形,求直線
為直角三角形,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() 的底面是菱形,
的底面是菱形,![]() 底面
底面![]() ,
,![]() 分別是
分別是![]() 的中點,
的中點,![]() ,
,![]() ,
,![]() .
.
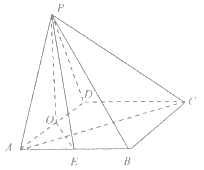
(I)證明:![]() ;
;
(II)求直線![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;
(III)在![]() 邊上是否存在點
邊上是否存在點![]() ,使
,使![]() 與
與![]() 所成角的余弦值為
所成角的余弦值為![]() ,若存在,確定點
,若存在,確定點![]() 位置;若不存在,說明理由.
位置;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,菱形![]() 中,
中,![]() ,
,![]() ,
,![]() 于
于![]() .將
.將![]() 沿
沿![]() 翻折到
翻折到![]() ,使
,使![]() ,如圖2.
,如圖2.

(Ⅰ)求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)求直線A′E與平面A′BC所成角的正弦值;
(Ⅲ)設![]() 為線段
為線段![]() 上一點,若
上一點,若![]() 平面
平面![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商場營銷人員進行某商品的市場營銷調查時發現,每回饋消費者一定的點數,該商品每天的銷量就會發生一定的變化,經過試點統計得到以下表:
反饋點數t | 1 | 2 | 3 | 4 | 5 |
銷量(百件)/天 | 0.5 | 0.6 | 1 | 1.4 | 1.7 |
(Ⅰ)經分析發現,可用線性回歸模型![]() 擬合當地該商品銷量
擬合當地該商品銷量![]() (千件)與返還點數
(千件)與返還點數![]() 之間的相關關系.試預測若返回6個點時該商品每天的銷量;
之間的相關關系.試預測若返回6個點時該商品每天的銷量;
(Ⅱ)若節日期間營銷部對商品進行新一輪調整.已知某地擬購買該商品的消費群體十分龐大,經營銷調研機構對其中的200名消費者的返點數額的心理預期值進行了一個抽樣調查,得到如下一份頻數表:
返還點數預期值區間 (百分比) | [1,3) | [3,5) | [5,7) | [7,9) | [9,11) | [11,13) |
頻數 | 20 | 60 | 60 | 30 | 20 | 10 |
(1)求這200位擬購買該商品的消費者對返點點數的心理預期值![]() 的樣本平均數及中位數的估計值(同一區間的預期值可用該區間的中點值代替;估計值精確到0.1);
的樣本平均數及中位數的估計值(同一區間的預期值可用該區間的中點值代替;估計值精確到0.1);
(2)將對返點點數的心理預期值在![]() 和
和![]() 的消費者分別定義為“欲望緊縮型”消費者和“欲望膨脹型”消費者,現采用分層抽樣的方法從位于這兩個區間的30名消費者中隨機抽取6名,再從這6人中隨機抽取3名進行跟蹤調查,設抽出的3人中 “欲望緊縮型”消費者的人數為隨機變量
的消費者分別定義為“欲望緊縮型”消費者和“欲望膨脹型”消費者,現采用分層抽樣的方法從位于這兩個區間的30名消費者中隨機抽取6名,再從這6人中隨機抽取3名進行跟蹤調查,設抽出的3人中 “欲望緊縮型”消費者的人數為隨機變量![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知動點![]() 滿足
滿足![]() ,記M的軌跡為曲線C,直線l:
,記M的軌跡為曲線C,直線l:![]() (
(![]() )交曲線C于P,Q兩點,點P在第一象限,
)交曲線C于P,Q兩點,點P在第一象限,![]() 軸,垂足為E,連接QE并延長交曲線C于點G.
軸,垂足為E,連接QE并延長交曲線C于點G.
(1)求曲線C的方程,并說明曲線C是什么曲線;
(2)若![]() ,求
,求![]() 的面積.
的面積.
(3)求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,內角A、B、C所對的邊分別為a、b、c,且sinAsinBcosB+sin2BcosA=2![]() sinCcosB.
sinCcosB.
(1)求tanB的值;
(2)若△ABC的外接圓半徑為R,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com