
【題目】已知動點![]() 滿足
滿足![]() ,記M的軌跡為曲線C,直線l:
,記M的軌跡為曲線C,直線l:![]() (
(![]() )交曲線C于P,Q兩點,點P在第一象限,
)交曲線C于P,Q兩點,點P在第一象限,![]() 軸,垂足為E,連接QE并延長交曲線C于點G.
軸,垂足為E,連接QE并延長交曲線C于點G.
(1)求曲線C的方程,并說明曲線C是什么曲線;
(2)若![]() ,求
,求![]() 的面積.
的面積.
(3)求![]() 面積的最大值.
面積的最大值.
【答案】(1)![]() ,軌跡是以
,軌跡是以![]() 、
、![]() 為焦點的橢圓
為焦點的橢圓
(2)![]()
(3)![]()
【解析】
(1)根據![]() ,由兩點間的距離公式可看出,其表示動點
,由兩點間的距離公式可看出,其表示動點![]() 與兩定點
與兩定點![]() 、
、![]() 的距離之和為
的距離之和為![]() ,且
,且![]() ,可知其符合橢圓的定義,把相關量代入橢圓標準方程,即可求解;
,可知其符合橢圓的定義,把相關量代入橢圓標準方程,即可求解;
(2)寫出直線![]() 的方程與曲線
的方程與曲線![]() 的方程聯立,便可解出點
的方程聯立,便可解出點![]() 坐標,進而知道點
坐標,進而知道點![]() 的坐標,再求出直線
的坐標,再求出直線![]() 的方程后,與曲線
的方程后,與曲線![]() 的方程聯立,可解出點
的方程聯立,可解出點![]() 的坐標,再代
的坐標,再代![]() 公式,即可求出面積;
公式,即可求出面積;
(3)將直線![]() 的方程與曲線
的方程與曲線![]() 的方程聯立,解出點
的方程聯立,解出點![]() 坐標,進而得點
坐標,進而得點![]() 的坐標,再求出直線
的坐標,再求出直線![]() 的方程后,與曲線
的方程后,與曲線![]() 的方程聯立,可得點
的方程聯立,可得點![]() 坐標,再根據點
坐標,再根據點![]() 坐標,得直線
坐標,得直線![]() 的斜率,可驗證
的斜率,可驗證![]() ,得
,得![]() 是直角三角形,代兩點間的距離公式可求出
是直角三角形,代兩點間的距離公式可求出![]() ,所以
,所以![]() 是一個關于直線
是一個關于直線![]() 的斜率的函數,由函數求最值的方法,即可求解.
的斜率的函數,由函數求最值的方法,即可求解.
(1)由![]() ,可得點
,可得點![]() 到點
到點![]() 、
、![]() 的距離之和為4且
的距離之和為4且![]() ,所以動點
,所以動點![]() 的軌跡是以
的軌跡是以![]() 、
、![]() 的橢圓,其中
的橢圓,其中![]() ,
,![]() ,即
,即![]() ,
,![]() ,所以曲線C的軌跡方程為
,所以曲線C的軌跡方程為![]() ,軌跡是以
,軌跡是以![]() 、
、![]() 的橢圓.
的橢圓.
(2)根據題![]() 意得,與
意得,與![]() 聯立
聯立
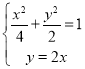 ,解得
,解得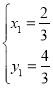 或
或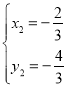
所以P點坐標為![]() ,Q點坐標為
,Q點坐標為![]()
因為![]() 軸,垂足為E,所以E點坐標為
軸,垂足為E,所以E點坐標為![]()
所以直線QE方程為![]()
與![]() 聯立,可得
聯立,可得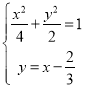 ,整理可得
,整理可得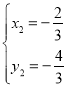 或
或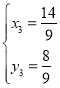
所以G點坐標為![]()
![]()
(3)設直線PQ的斜率為k,則其方程為![]() (
(![]() ).由
).由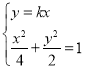 得
得![]() .
.
記![]() ,則
,則![]() ,
,![]() ,
,![]() .
.
于是直線QG的斜率為![]() ,方程為
,方程為![]() .
.
由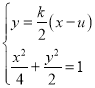 得
得![]() ——①
——①
設![]() ,則
,則![]() 和
和![]() 是方程①的解,故
是方程①的解,故![]() .由此得
.由此得![]() .
.
從而直線PG的斜率為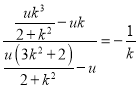 .
.
所以![]() ,即
,即![]() 是直角三角形.
是直角三角形.
得![]() ,
,![]() .
.
所以![]() 的面積
的面積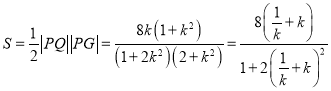 .
.
設![]() ,則由
,則由![]() 得
得![]() ,當且僅當
,當且僅當![]() 時取等號.
時取等號.
因為![]() 在
在![]() 單調遞減,所以當
單調遞減,所以當![]() ,即
,即![]() 時,S取得最大值,最大值為
時,S取得最大值,最大值為![]() .
.
因此,![]() 面積的最大值為
面積的最大值為![]() .
.


 長江作業本同步練習冊系列答案
長江作業本同步練習冊系列答案科目:高中數學 來源: 題型:
【題目】如圖,某海面上有![]() 、
、![]() 、
、![]() 三個小島(面積大小忽略不計),
三個小島(面積大小忽略不計),![]() 島在
島在![]() 島的北偏東
島的北偏東![]() 方向距
方向距![]() 島
島![]() 千米處,
千米處,![]() 島在
島在![]() 島的正東方向距
島的正東方向距![]() 島20千米處.以
島20千米處.以![]() 為坐標原點,
為坐標原點,![]() 的正東方向為
的正東方向為![]() 軸的正方向,1千米為單位長度,建立平面直角坐標系.圓
軸的正方向,1千米為單位長度,建立平面直角坐標系.圓![]() 經過
經過![]() 、
、![]() 、
、![]() 三點.
三點.

(1)求圓![]() 的方程;
的方程;
(2)若圓![]() 區域內有未知暗礁,現有一船D在
區域內有未知暗礁,現有一船D在![]() 島的南偏西30°方向距
島的南偏西30°方向距![]() 島40千米處,正沿著北偏東
島40千米處,正沿著北偏東![]() 行駛,若不改變方向,試問該船有沒有觸礁的危險?
行駛,若不改變方向,試問該船有沒有觸礁的危險?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】教材曾有介紹:圓![]() 上的點
上的點![]() 處的切線方程為
處的切線方程為![]() 。我們將其結論推廣:橢圓
。我們將其結論推廣:橢圓![]() 上的點
上的點![]() 處的切線方程為
處的切線方程為![]() ,在解本題時可以直接應用。已知,直線
,在解本題時可以直接應用。已知,直線![]() 與橢圓
與橢圓![]() 有且只有一個公共點.
有且只有一個公共點.
(1)求![]() 的值;
的值;
(2)設![]() 為坐標原點,過橢圓
為坐標原點,過橢圓![]() 上的兩點
上的兩點![]() 、
、![]() 分別作該橢圓的兩條切線
分別作該橢圓的兩條切線![]() 、
、![]() ,且
,且![]() 與
與![]() 交于點
交于點![]() 。當
。當![]() 變化時,求
變化時,求![]() 面積的最大值;
面積的最大值;
(3)在(2)的條件下,經過點![]() 作直線
作直線![]() 與該橢圓
與該橢圓![]() 交于
交于![]() 、
、![]() 兩點,在線段
兩點,在線段![]() 上存在點
上存在點![]() ,使
,使![]() 成立,試問:點
成立,試問:點![]() 是否在直線
是否在直線![]() 上,請說明理由.
上,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,離心率為
,離心率為![]() ,過焦點
,過焦點![]() 且垂直于
且垂直于![]() 軸的直線被橢圓
軸的直線被橢圓![]() 截得的線段長為
截得的線段長為![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)點![]() 為橢圓
為橢圓![]() 上一動點,連接
上一動點,連接![]() 、
、![]() ,設
,設![]() 的角平分線
的角平分線![]() 交橢圓
交橢圓![]() 的長軸于點
的長軸于點![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某調查機構對全國互聯網行業進行調查統計,得到整個互聯網行業從業者年齡分布餅狀圖、90后從事互聯網行業者崗位分布條形圖,則下列結論中不一定正確的是( ).
注:90后指1990年及以后出生,80后指1980-1989年之間出生,80前指1979年及以前出生.

A. 互聯網行業從業人員中90后占一半以上
B. 互聯網行業中從事技術崗位的人數超過總人數的20%
C. 互聯網行業中從事運營崗位的人數90后比80前多
D. 互聯網行業中從事技術崗位的人數90后比80后多
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某書店剛剛上市了《中國古代數學史》,銷售前該書店擬定了5種單價進行試銷,每種單價(![]() 元)試銷l天,得到如表單價
元)試銷l天,得到如表單價![]() (元)與銷量
(元)與銷量![]() (冊)數據:
(冊)數據:
單價 | 18 | 19 | 20 | 21 | 22 |
銷量 | 61 | 56 | 50 | 48 | 45 |
(l)根據表中數據,請建立![]() 關于
關于![]() 的回歸直線方程:
的回歸直線方程:
(2)預計今后的銷售中,銷量![]() (冊)與單價
(冊)與單價![]() (元)服從(l)中的回歸方程,已知每冊書的成本是12元,書店為了獲得最大利潤,該冊書的單價應定為多少元?
(元)服從(l)中的回歸方程,已知每冊書的成本是12元,書店為了獲得最大利潤,該冊書的單價應定為多少元?
附: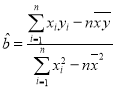 ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,平面上定點![]() 到定直線
到定直線![]() 的距離
的距離![]() ,
,![]() 為該平面上的動點,過
為該平面上的動點,過![]() 作直線
作直線![]() 的垂線,垂足為
的垂線,垂足為![]() ,且
,且![]() ;
;

(1)試建立適當的平面直角坐標系,求動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)過點![]() 的直線交軌跡
的直線交軌跡![]() 于
于![]() 、
、![]() 兩點,交直線
兩點,交直線![]() 于點
于點![]() ,已知
,已知![]() ,
,![]() ,求證:
,求證:![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C所對的邊分別為a,b,c.滿足2acosC+bcosC+ccosB=0.
(Ⅰ)求角C的大小;
(Ⅱ)若a=2,△ABC的面積為![]() ,求C的大小。
,求C的大小。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com