
【題目】已知函數f(x)=ax(lnx﹣1)﹣x2(a∈R)恰有兩個極值點x1 , x2 , 且x1<x2 . (Ⅰ)求實數a的取值范圍;
(Ⅱ)若不等式lnx1+λlnx2>1+λ恒成立,求實數λ的取值范圍.
【答案】解:(Ⅰ)∵f(x)=ax(lnx﹣1)﹣x2(a∈R), ∴f′(x)=alnx﹣2x,
依題意得x1 , x2是alnx﹣2x=0的兩個不等正實數根,
∴a≠0, ![]() ,
,
令g(x)= ![]() ,
, ![]() ,
,
當x∈(0,e)時,g′(x)>0;當x∈(e,+∞)時,g′(x)<0,
∴g(x)在(0,e)上單調遞增,在(e,+∞)上單調遞減,且g(1)=0,
當x>e時,g(x)>0,
∴0< ![]() <g(e)=
<g(e)= ![]() ,
,
解得a>2e,故實數a的取值范圍是(2e,+∞).
(Ⅱ)由(Ⅰ)得alnx1=2x1 , alnx2=2x2 ,
兩式相減,得a(lnx1﹣lnx2)=2(x1﹣x2),a=2 ![]() ,
,
∴lnx1+λlnx2>1+λ,∴ ![]() >1+λ,∴2(x1+λx2)>a(1+λ),
>1+λ,∴2(x1+λx2)>a(1+λ),
∴x1+λx2> ![]() ,∴
,∴ ![]() >1+λ,
>1+λ,
∴ 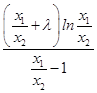 >1+λ,
>1+λ,
∵0<x1<x2 , 令t= ![]() ∈(0,1),∴
∈(0,1),∴ ![]() ,
,
∴(t+λ)lnt﹣(1+λ)(t﹣1)<0,
令h(t)=(t+λ)lnt﹣(1+λ)(t﹣1),
則h′(t)=lnt+ ![]() ﹣λ,
﹣λ,
令I(t)=lnt+ ![]() ﹣λ,則I′(t)=
﹣λ,則I′(t)= ![]() =
= ![]() ,(t∈(0,1)),
,(t∈(0,1)),
①當λ≥1時,I′(t)<0,∴h′(t)在(0,1)上單調遞減,∴h′(t)>h′(1)=0,
∴h(t)在(0,1)上單調遞增,∴h(t)<h(1)=0,符合題意.
②當λ≤0時,I′(t)>0.∴h′(t)在(0,1)上單調遞增,∴h′(t)<h′(1)=0,
∴h′(t)在(0,1)上單調遞減,∴h(t)>h(1)=0,不符合題意
③當0<λ<1時,I′(t)>0,λ<t<1,∴h′(t)在(λ,1)上單調遞增,
∴h′(t)<h′(1)=0,
∴h(t)在(λ,1)上單調遞減,∴h(t)>h(1)=0,不符合題意.
綜上所述,實數λ的取值范圍是[1,+∞).
【解析】(Ⅰ)求出f′(x)=alnx﹣2x,a≠0, ![]() ,令g(x)=
,令g(x)= ![]() ,
, ![]() ,由此利用導數性質能求出實數a的取值范圍.(Ⅱ)由(Ⅰ)得alnx1=2x1 , alnx2=2x2 , 兩式相減,得a(lnx1﹣lnx2)=2(x1﹣x2),a=2
,由此利用導數性質能求出實數a的取值范圍.(Ⅱ)由(Ⅰ)得alnx1=2x1 , alnx2=2x2 , 兩式相減,得a(lnx1﹣lnx2)=2(x1﹣x2),a=2 ![]() ,從而
,從而  >1+λ,令t=
>1+λ,令t= ![]() ∈(0,1),得(t+λ)lnt﹣(1+λ)(t﹣1)<0,令h(t)=(t+λ)lnt﹣(1+λ)(t﹣1),則h′(t)=lnt+
∈(0,1),得(t+λ)lnt﹣(1+λ)(t﹣1)<0,令h(t)=(t+λ)lnt﹣(1+λ)(t﹣1),則h′(t)=lnt+ ![]() ﹣λ,令I(t)=lnt+
﹣λ,令I(t)=lnt+ ![]() ﹣λ,則I′(t)=
﹣λ,則I′(t)= ![]() =
= ![]() ,(t∈(0,1)),由此利用分類討論思想,結合導數性質能求出實數λ的取值范圍.
,(t∈(0,1)),由此利用分類討論思想,結合導數性質能求出實數λ的取值范圍.
【考點精析】根據題目的已知條件,利用函數的極值與導數和函數的最大(小)值與導數的相關知識可以得到問題的答案,需要掌握求函數![]() 的極值的方法是:(1)如果在
的極值的方法是:(1)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極大值(2)如果在
是極大值(2)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極小值;求函數
是極小值;求函數![]() 在
在![]() 上的最大值與最小值的步驟:(1)求函數
上的最大值與最小值的步驟:(1)求函數![]() 在
在![]() 內的極值;(2)將函數
內的極值;(2)將函數![]() 的各極值與端點處的函數值
的各極值與端點處的函數值![]() ,
,![]() 比較,其中最大的是一個最大值,最小的是最小值.
比較,其中最大的是一個最大值,最小的是最小值.


 能考試全能100分系列答案
能考試全能100分系列答案科目:高中數學 來源: 題型:
【題目】九十年代,政府間氣候變化專業委員會(IPCC)提供的一項報告指出:使全球氣候逐年變暖的一個重要因素是人類在能源利用與森林砍伐中使CO2濃度增加.據測,1990年、1991年、1992年大氣中的CO2濃度分別比1989年增加了1個可比單位、3個可比單位、6個可比單位。若用函數模擬九十年代中每年CO2濃度增加的可比單位數y與年份增加數x的關系,模擬函數可選用二次函數或函數![]() (其中a、b、c為常數).
(其中a、b、c為常數).
(Ⅰ)寫出這兩個函數的解釋式;
(Ⅱ)若知1994年大氣中的CO2濃度比1989年增加了16個可比單位,請問用以上哪個函數作為模擬函數與1994年的實際數據更接近?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國是世界上嚴重缺水的國家,某市為了制定合理的節水方案,對居民用水情況進行了調查,通過抽樣,獲得了某年100位居民每人的月均用水量![]() 單位:噸
單位:噸![]() ,將數據按照
,將數據按照![]() ,
,![]() ,
,![]() 分成9組,制成了如圖所示的頻率分布直方圖.
分成9組,制成了如圖所示的頻率分布直方圖.
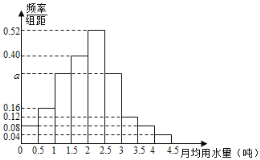
(1)設該市有30萬居民,估計全市居民中月均用水量不低于3噸的人數![]() 說明理由;
說明理由;
(2)估計居民月均用水量的中位數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某研究型學習小組調查研究高中生使用智能手機對學習的影響,部分統計數據如下:
使用智能手機 | 不使用智能手機 | 合計 | |
學習成績優秀 |
|
| |
學習成績不優秀 |
|
| |
合計 |
(1)根據以上統計數據,你是否有![]() 的把握認為使用智能手機對學習有影響?
的把握認為使用智能手機對學習有影響?
(2)為了進一步了解學生對智能手機的使用習慣,現在對以上使用智能手機的高中時采用分層抽樣的方式,抽取一個容量為![]() 的樣本,若抽到的學生中成績不優秀的比成績優秀的多
的樣本,若抽到的學生中成績不優秀的比成績優秀的多![]() 人,求
人,求![]() 的值.
的值.
|
|
|
|
|
|
|
|
|
|
|
|
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設集合A={x|x2-3x+2=0},B={x|x2+(a-1)x+a2-5=0}.
(1)若A∩B={2},求實數a的值;
(2)若A∪B=A,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=sinωxcosωx﹣ ![]() (ω>0)圖象的兩條相鄰對稱軸為
(ω>0)圖象的兩條相鄰對稱軸為 ![]() .
.
(1)求函數y=f(x)的對稱軸方程;
(2)若函數y=f(x)﹣ ![]() 在(0,π)上的零點為x1 , x2 , 求cos(x1﹣x2)的值.
在(0,π)上的零點為x1 , x2 , 求cos(x1﹣x2)的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知二次函數![]() ,則下列說法不正確的是( )
,則下列說法不正確的是( )
A.其圖象開口向上,且始終與![]() 軸有兩個不同的交點
軸有兩個不同的交點
B.無論![]() 取何實數,其圖象始終過定點
取何實數,其圖象始終過定點![]()
C.其圖象對稱軸的位置沒有確定,但其形狀不會因![]() 的取值不同而改變
的取值不同而改變
D.函數的最小值大于![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com