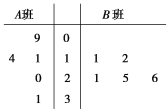
【題目】某校為了解A，B兩班學生手機上網的時長，分別從這兩個班中隨機抽取5名同學進行調查，將他們平均每周手機上網的時長作為樣本，繪制成莖葉圖如圖所示（圖中的莖表示十位數字，葉表示個位數字）．
(1) 試估計哪個班級學生平均上網的時間較長。
(2)從A班的樣本數據中隨機抽取一個不超過19的數據記為a，從B班的樣本數據中隨機抽取一個不超過21的數據記為b，求a＞b的概率．
【答案】（1）B班;（2）
【解析】
(1)直接計算兩班的上網時間的平均值，再比較即得解；（2）直接利用古典概型的概率公式求解.
(1)A班樣本數據的平均值為
(9＋11＋14＋20＋31)＝17.
由此估計A班學生每周平均上網時間為17小時；
B班樣本數據的平均值為(11＋12＋21＋25＋26)＝19，
由此估計B班學生每周平均上網時間較長.
(2)A班的樣本數據中不超過19的數據a有3個，分別為9,11,14，
B班的樣本數據中不超過21的數據b也有3個，分別為11,12,21，
從A班和B班的樣本數據中各隨機抽取一個共有9種不同情況，
分別為(9,11)，(9,12)，(9,21)，(11,11)，(11,12)，(11,21)，(14,11)，(14,12)，(14,21)，
其中a＞b的情況有(14,11)，(14,12)兩種，
故a＞b的概率p＝.
智慧課堂密卷100分單元過關檢測系列答案科目：高中數學 來源： 題型：
【題目】甲乙兩名運動員互不影響地進行四次設計訓練，根據以往的數據統計，他們設計成績均不低于8環（成績環數以整數計），且甲乙射擊成績（環數）的分布列如下：
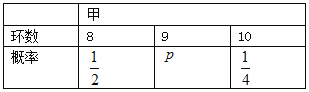
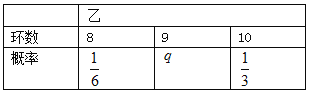
（I）求
， 
的值；
（II）若甲乙兩射手各射擊兩次，求四次射擊中恰有三次命中9環的概率；
（III）若兩個射手各射擊1次，記兩人所得環數的差的絕對值為
，求
的分布列和數學期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，正方體
的棱長為1，線段
上有兩個動點
，且
，現有如下四個結論：
；
平面
；
三棱錐
的體積為定值；
異面直線
所成的角為定值，
其中正確結論的序號是______．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為鼓勵居民節約用水，某市自來水公司對全市用戶采用分段計費的方式計算水費，收費標準如下：不超過
的部分為2.20元/
；超過不超過
的部分為2.80元/；超過部分為3.20元/.
（1）試求居民月水費y（元）關于用水量
的函數關系式；
（2）某戶居民4月份用水
，應交水費多少元？
（3）若有一戶居民5月份水費為57.20元，請問該戶居民5月份用水多少？
（4）若某戶居民6月份、7月份共用水
，且6月份水費比7月份水費少12元，則該戶居民6、7月份各用水多少？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某物流公司欲將一批海產品從A地運往B地，現有汽車、火車、飛機三種運輸工具可供選擇，這三種工具的主要參考數據如下：
運輸工具 | 途中速度（ | 途中費用（元/ | 裝卸時間（ | 裝卸費用（元/ |
汽車 | 50 | 80 | 2 | 200 |
火車 | 100 | 40 | 3 | 400 |
飛機 | 200 | 200 | 3 | 800 |
若這批海產品在運輸過程中的損耗為300元/
，問采用哪種運輸方式比較好，即運輸過程中的費用與損耗之和最小.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某企業甲,乙兩個研發小組,他們研發新產品成功的概率分別為
和
,現安排甲組研發新產品
,乙組研發新產品
.設甲,乙兩組的研發是相互獨立的.
(1)求至少有一種新產品研發成功的概率;
(2)若新產品
研發成功,預計企業可獲得
萬元,若新產品
研發成功,預計企業可獲得利潤
萬元,求該企業可獲得利潤的分布列和數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
