
【題目】某物流公司欲將一批海產品從A地運往B地,現有汽車、火車、飛機三種運輸工具可供選擇,這三種工具的主要參考數據如下:
運輸工具 | 途中速度( | 途中費用(元/ | 裝卸時間( | 裝卸費用(元/ |
汽車 | 50 | 80 | 2 | 200 |
火車 | 100 | 40 | 3 | 400 |
飛機 | 200 | 200 | 3 | 800 |
若這批海產品在運輸過程中的損耗為300元/![]() ,問采用哪種運輸方式比較好,即運輸過程中的費用與損耗之和最小.
,問采用哪種運輸方式比較好,即運輸過程中的費用與損耗之和最小.
科目:高中數學 來源: 題型:
【題目】(本小題滿分12分)某公司為確定下一年度投入某種產品的宣傳費,需了解年宣傳費x(單位:千元)對年銷售量y(單位:t)和年利潤z(單位:千元)的影響,對近8年的宣傳費![]() 和年銷售量
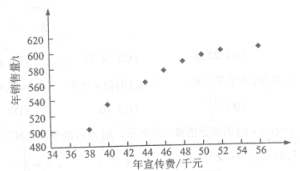
和年銷售量![]() 數據作了初步處理,得到下面的散點圖及一些統計量的值.
數據作了初步處理,得到下面的散點圖及一些統計量的值.
|
|
|
|
|
|
|
46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
表中![]() =
=![]() ,
,![]() =
=![]()
![]()
(Ⅰ)根據散點圖判斷,![]() 與
與![]()
(Ⅱ)根據(Ⅰ)的判斷結果及表中數據,建立y關于x的回歸方程;
(III)已知這種產品的年利潤z與x,y的關系為![]() ,根據(Ⅱ)的結果回答下列問題:
,根據(Ⅱ)的結果回答下列問題:
(Ⅰ)當年宣傳費![]() 時,年銷售量及年利潤的預報值時多少?
時,年銷售量及年利潤的預報值時多少?
(Ⅱ)當年宣傳費![]() 為何值時,年利潤的預報值最大?
為何值時,年利潤的預報值最大?
附:對于一組數據![]() ,
,![]() ,……,
,……,![]() ,其回歸線
,其回歸線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為:
 ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】前幾年隨著網購的普及,線下零售遭遇挑戰,但隨著新零售模式的不斷出現,零售行業近幾年呈現增長趨勢,下表為![]() 年中國百貨零售業銷售額(單位:億元,數據經過處理,
年中國百貨零售業銷售額(單位:億元,數據經過處理, ![]() 分別對應
分別對應![]() ):
):
年份代碼 | 1 | 2 | 3 | 4 |
銷售額 | 95 | 165 | 230 | 310 |
(1)由上表數據可知,可用線性回歸模型擬合![]() 與
與![]() 的關系,請用相關系數加以說明;
的關系,請用相關系數加以說明;
(2)建立![]() 關于
關于![]() 的回歸方程,并預測2018年我國百貨零售業銷售額;
的回歸方程,并預測2018年我國百貨零售業銷售額;
(3)從![]() 年這4年的百貨零售業銷售額及2018年預測銷售額這5個數據中任取2個數據,求這2個數據之差的絕對值大于200億元的概率.
年這4年的百貨零售業銷售額及2018年預測銷售額這5個數據中任取2個數據,求這2個數據之差的絕對值大于200億元的概率.
參考數據:
![]() ,
, 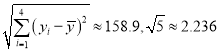
參考公式:相關系數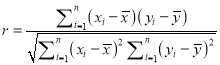 ,回歸方程
,回歸方程![]() 中斜率和截距的最小二乘估計公式分別為
中斜率和截距的最小二乘估計公式分別為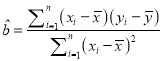 ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
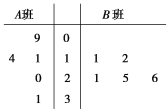
【題目】某校為了解A,B兩班學生手機上網的時長,分別從這兩個班中隨機抽取5名同學進行調查,將他們平均每周手機上網的時長作為樣本,繪制成莖葉圖如圖所示(圖中的莖表示十位數字,葉表示個位數字).
(1) 試估計哪個班級學生平均上網的時間較長。
(2)從A班的樣本數據中隨機抽取一個不超過19的數據記為a,從B班的樣本數據中隨機抽取一個不超過21的數據記為b,求a>b的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ex(x2+ax-a),其中a是常數.
(1)當a=1時,求曲線y=f(x)在點(1,f(1))處的切線方程;
(2)若存在實數k,使得關于x的方程f(x)=k在[0,+∞)上有兩個不相等的實數根,求k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商店為了解氣溫對某產品銷售量的影響,隨機記錄了該商店![]() 月份中
月份中![]() 天的日銷售量
天的日銷售量![]() (單位:千克)與該地當日最低氣溫
(單位:千克)與該地當日最低氣溫![]() (單位:℃)的數據,如表所示:
(單位:℃)的數據,如表所示:
|
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 與
與![]() 的回歸方程
的回歸方程![]() :
:
(2)判斷![]() 與
與![]() 之間是正相關還是負相關;若該地
之間是正相關還是負相關;若該地![]() 月份某天的最低氣溫為
月份某天的最低氣溫為![]() ,請用(1)中的回歸方程預測該商店當日的銷售量.
,請用(1)中的回歸方程預測該商店當日的銷售量.
參考公式: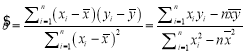 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以原點
為參數),以原點![]() 為極點,
為極點, ![]() 軸的正半軸為極軸,建立極坐標系,曲線
軸的正半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程
的極坐標方程![]() .
.
(1)求直線![]() 的普通方程及曲線
的普通方程及曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設曲線![]() 與
與![]() 軸的兩個交點分別為
軸的兩個交點分別為![]() ,與
,與![]() 軸正半軸的交點為
軸正半軸的交點為![]() ,求直線
,求直線![]() 將
將![]() 分成的兩部分的面積比.
分成的兩部分的面積比.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() (
(![]() )的離心率為
)的離心率為![]() ,圓
,圓![]() 與
與![]() 軸正半軸交于點
軸正半軸交于點![]() ,圓
,圓![]() 在點
在點![]() 處的切線被橢圓
處的切線被橢圓![]() 截得的弦長為
截得的弦長為![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)設圓![]() 上任意一點
上任意一點![]() 處的切線交橢圓
處的切線交橢圓![]() 于點
于點![]() ,試判斷
,試判斷![]() 是否為定值?若為定值,求出該定值;若不是定值,請說明理由.
是否為定值?若為定值,求出該定值;若不是定值,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com