
【題目】某商店為了解氣溫對某產(chǎn)品銷售量的影響,隨機記錄了該商店![]() 月份中
月份中![]() 天的日銷售量
天的日銷售量![]() (單位:千克)與該地當日最低氣溫
(單位:千克)與該地當日最低氣溫![]() (單位:℃)的數(shù)據(jù),如表所示:
(單位:℃)的數(shù)據(jù),如表所示:
|
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 與
與![]() 的回歸方程
的回歸方程![]() :
:
(2)判斷![]() 與
與![]() 之間是正相關還是負相關;若該地
之間是正相關還是負相關;若該地![]() 月份某天的最低氣溫為
月份某天的最低氣溫為![]() ,請用(1)中的回歸方程預測該商店當日的銷售量.
,請用(1)中的回歸方程預測該商店當日的銷售量.
參考公式: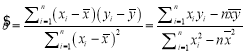 ,
,![]() .
.
【答案】(1)![]() ; (2)y與x之間是負相關,預測該商店當日的銷售量為9.56千克.
; (2)y與x之間是負相關,預測該商店當日的銷售量為9.56千克.
【解析】
(1)根據(jù)表中的數(shù)據(jù)求出![]() 等數(shù)據(jù),從而求出
等數(shù)據(jù),從而求出![]() ,
,![]() 值,進而得出回歸方程;
值,進而得出回歸方程;
(2)根據(jù)(1)的方程可得y與x之間的相關關系,將![]() 代入回歸方程,即可預測當日的銷售量.
代入回歸方程,即可預測當日的銷售量.
解:(1)根據(jù)表中信息,![]() =
=![]() =7,
=7,![]() =
=![]() =9,
=9,
![]() =287,
=287,![]() =295,
=295,
所以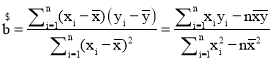 =
=![]() =-0.56,
=-0.56,
所以![]() =9+0.56×7=12.92.
=9+0.56×7=12.92.
所以y與x的回歸方程![]() .
.
(2)由(1)知,y與x之間是負相關,
根據(jù)回歸方程當x=6時,
![]() =-0.56x+12.92=9.56,
=-0.56x+12.92=9.56,
答:預測該商店當日的銷售量為16.28千克.


科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]()
![]() .
.
(1)當![]() 時,若函數(shù)
時,若函數(shù)![]() 恰有一個零點,求實數(shù)
恰有一個零點,求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)當![]() ,
, ![]() 時,對任意
時,對任意![]() ,有
,有![]() 成立,求實數(shù)
成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設函數(shù)![]() .
.
(Ⅰ)求函數(shù)![]() 的單調(diào)區(qū)間和極值;
的單調(diào)區(qū)間和極值;
(Ⅱ)當![]() 時,若函數(shù)
時,若函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上存在唯一零點,求
上存在唯一零點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】下列說法的錯誤的是( )
A. 經(jīng)過定點![]() 的傾斜角不為
的傾斜角不為![]() 的直線的方程都可以表示為
的直線的方程都可以表示為![]()
B. 經(jīng)過定點![]() 的傾斜角不為
的傾斜角不為![]() 的直線的方程都可以表示為
的直線的方程都可以表示為![]()
C. 不經(jīng)過原點的直線的方程都可以表示為![]()
D. 經(jīng)過任意兩個不同的點![]() 、
、![]() 直線的方程都可以表示為
直線的方程都可以表示為![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】給出下列結論:
(1)某學校從編號依次為001,002,…,900的900個學生中用系統(tǒng)抽樣的方法抽取一個樣本,已知樣本中有兩個相鄰的編號分別為053,098,則樣本中最大的編號為862.
(2)甲組數(shù)據(jù)的方差為5,乙組數(shù)據(jù)為5、6、9、10、5,那么這兩組數(shù)據(jù)中較穩(wěn)定的是甲.
(3)若兩個變量的線性相關性越強,則相關系數(shù)![]() 的值越接近于1.
的值越接近于1.
(4)對A、B、C三種個體按3:1:2的比例進行分層抽樣調(diào)查,若抽取的A種個體有15個,則樣本容量為30.
則正確的個數(shù)是
A. 3 B. 2 C. 1 D. 0
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,有一個水平放置的透明無蓋的正方體容器,容器高8cm,將一個球放在容器口,再向容器注水,當球面恰好接觸水面時測得水深為6cm,如不計容器的厚度,則球的體積為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設△AnBnCn的三邊長分別為an , bn , cn , △AnBnCn的面積為Sn , n=1,2,3…若b1>c1 , b1+c1=2a1 , an+1=an , ![]() ,
, ![]() ,則( )
,則( )
A.{Sn}為遞減數(shù)列
B.{Sn}為遞增數(shù)列
C.{S2n﹣1}為遞增數(shù)列,{S2n}為遞減數(shù)列
D.{S2n﹣1}為遞減數(shù)列,{S2n}為遞增數(shù)列
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知一家公司生產(chǎn)某種品牌服裝的年固定成本為10萬元,每生產(chǎn)1千件需另投入2.7萬元.設該公司一年內(nèi)共生產(chǎn)該品牌服裝x千件并全部銷售完,每千件的銷售收入為![]() 萬元,且
萬元,且 .
.
(1)寫出年利潤W(萬元)關于年產(chǎn)量x(千件)的函數(shù)解析式;
(2)年產(chǎn)量為多少千件時,該公司在這一品牌服裝的生產(chǎn)中所獲得利潤最大?(注:年利潤=年銷售收入﹣年總成本)
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com