【題目】如圖，有一個水平放置的透明無蓋的正方體容器，容器高8cm，將一個球放在容器口，再向容器注水，當(dāng)球面恰好接觸水面時測得水深為6cm，如不計容器的厚度，則球的體積為（ ）
A.
B.
C.
D.
【答案】A
【解析】解：設(shè)正方體上底面所在平面截球得小圓M，
則圓心M為正方體上底面正方形的中心．如圖．
設(shè)球的半徑為R，根據(jù)題意得球心到上底面的距離等于（R﹣2）cm，
而圓M的半徑為4，由球的截面圓性質(zhì)，得R2=（R﹣2）2+42 ，
解出R=5，
∴根據(jù)球的體積公式，該球的體積V= 
= 
= 
．
故選A．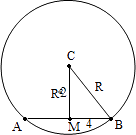
設(shè)正方體上底面所在平面截球得小圓M，可得圓心M為正方體上底面正方形的中心．設(shè)球的半徑為R，根據(jù)題意得球心到上底面的距離等于（R﹣2）cm，而圓M的半徑為4，由球的截面圓性質(zhì)建立關(guān)于R的方程并解出R=5，用球的體積公式即可算出該球的體積．
每日10分鐘口算心算速算天天練系列答案科目：高中數(shù)學(xué) 來源： 題型：
【題目】2015年推出一種新型家用轎車，購買時費用為16.9萬元，每年應(yīng)交付保險費、養(yǎng)路費及汽油費共1.2萬元，汽車的維修費為：第一年無維修費用，第二年為0.2萬元，從第三年起，每年的維修費均比上一年增加0.2萬元.
（I）設(shè)該輛轎車使用n年的總費用（包括購買費用、保險費、養(yǎng)路費、汽油費及維修費）為f(n)，求f(n)的表達式；
（II）這種汽車使用多少報廢最合算（即該車使用多少年，年平均費用最少）？
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在平面直角坐標(biāo)系
中，已知圓
的方程為
，
點的坐標(biāo)為
.
（1）求過點且與圓相切的直線方程；
（2）過點任作一條直線
與圓交于不同兩點
，
，且圓交
軸正半軸于點
，求證：直線
與
的斜率之和為定值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某商店為了解氣溫對某產(chǎn)品銷售量的影響，隨機記錄了該商店
月份中
天的日銷售量
（單位：千克）與該地當(dāng)日最低氣溫
（單位：℃）的數(shù)據(jù)，如表所示：
|
|
|
|
|
|
|
|
|
|
|
|
（1）求與的回歸方程
：
（2）判斷與之間是正相關(guān)還是負相關(guān)；若該地月份某天的最低氣溫為
，請用（1）中的回歸方程預(yù)測該商店當(dāng)日的銷售量．
參考公式：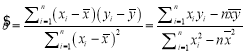
，
．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，三角形
所在的平面與長方形
所在的平面垂直，
.點
是
邊的中點，點
分別在線段
，
上，且
.
(1)證明：
；
(2)求二面角
的正切值；
(3)求直線
與直線PG所成角的余弦值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
（1）若不等式
的解集為
，求實數(shù)
的值；
（2）若不等式
對一切實數(shù)
恒成立，求實數(shù)的取值范圍；
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知⊙
的半徑為
，圓心的坐標(biāo)為
，其中
．
，
為該圓的兩條切線，
為坐標(biāo)原點，
，
為切點，在第一象限，在第四象限．
（）若
時，求切線，的斜率．
（
）若
時，求
外接圓的標(biāo)準(zhǔn)方程．
（
）當(dāng)點在
軸上運動時，將
表示成
的函數(shù)
，并求函數(shù)的最小值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知數(shù)列
滿足
，若
為單調(diào)遞增的等差數(shù)列，其前
項和為
，則
__________；若為單調(diào)遞減的等比數(shù)列，其前項和為
，則
__________.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
