
【題目】已知圓![]() 的圓心在射線
的圓心在射線![]() 上,截直線
上,截直線![]() 所得的弦長為6,且與直線
所得的弦長為6,且與直線![]() 相切.
相切.
(1)求圓![]() 的方程;
的方程;
(2)已知點![]() ,在直線
,在直線![]() 上是否存在點
上是否存在點![]() (異于點
(異于點![]() ),使得對圓
),使得對圓![]() 上的任一點
上的任一點![]() ,都有
,都有![]() 為定值
為定值![]() ?若存在,請求出點
?若存在,請求出點![]() 的坐標及
的坐標及![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
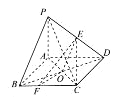
【題目】如圖所示,底面為正方形的四棱錐P-ABCD中,AB=2,PA=4,PB=PD=![]() ,AC與BD相交于點O,E為PD中點.
,AC與BD相交于點O,E為PD中點.
(1)求證:EO//平面PBC;
(2)設線段BC上點F滿足CF=2BF,求銳二面角E-OF-C的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】蘋果是人們日常生活中常見的營養型水果.某地水果批發市場銷售來自5個不同產地的富士蘋果,各產地的包裝規格相同,它們的批發價格(元/箱)和市場份額如下:
產地 |
|
|
|
|
|
批發價格 |
|
|
|
|
|
市場份額 |
|
|
|
|
|
市場份額亦稱“市場占有率”.指某一產品的銷售量在市場同類產品中所占比重.
(1)從該地批發市場銷售的富士蘋果中隨機抽取一箱,求該箱蘋果價格低于![]() 元的概率;
元的概率;
(2)按市場份額進行分層抽樣,隨機抽取![]() 箱富士蘋果進行檢驗,
箱富士蘋果進行檢驗,
①從產地![]() 共抽取
共抽取![]() 箱,求
箱,求![]() 的值;
的值;
②從這![]() 箱蘋果中隨機抽取兩箱進行等級檢驗,求兩箱產地不同的概率;
箱蘋果中隨機抽取兩箱進行等級檢驗,求兩箱產地不同的概率;
(3)由于受種植規模和蘋果品質的影響,預計明年產地![]() 的市場份額將增加
的市場份額將增加![]() ,產地
,產地![]() 的市場份額將減少
的市場份額將減少![]() ,其它產地的市場份額不變,蘋果銷售價格也不變(不考慮其它因素).設今年蘋果的平均批發價為每箱
,其它產地的市場份額不變,蘋果銷售價格也不變(不考慮其它因素).設今年蘋果的平均批發價為每箱![]() 元,明年蘋果的平均批發價為每箱
元,明年蘋果的平均批發價為每箱![]() 元,比較
元,比較![]() 的大小.(只需寫出結論)
的大小.(只需寫出結論)
查看答案和解析>>
科目:高中數學 來源: 題型:
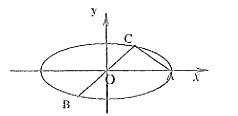
【題目】如圖已知橢圓![]() ,
,![]() 是長軸的一個端點,弦
是長軸的一個端點,弦![]() 過橢圓的中心
過橢圓的中心![]() ,且
,且![]() ,
,![]() .
.
(Ⅰ)求橢圓的方程:
(Ⅱ)設![]() 為橢圓上異于
為橢圓上異于![]() 且不重合的兩點,且
且不重合的兩點,且![]() 的平分線總是垂直于
的平分線總是垂直于![]() 軸,是否存在實數
軸,是否存在實數![]() ,使得
,使得![]() ,若存在,請求出
,若存在,請求出![]() 的最大值,若不存在,請說明理由.
的最大值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,![]() 是通過某城市開發區中心O的兩條南北和東西走向的街道,連結M,N兩地之間的鐵路線是圓心在
是通過某城市開發區中心O的兩條南北和東西走向的街道,連結M,N兩地之間的鐵路線是圓心在![]() 上的一段圓弧,若點M在點O正北方向3公里;點N到的
上的一段圓弧,若點M在點O正北方向3公里;點N到的![]() 距離分別為4公里和5公里.
距離分別為4公里和5公里.
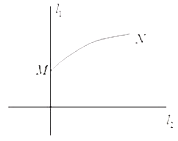
(1)建立適當的坐標系,求鐵路線所在圓弧的方程;
(2)若該城市的某中學擬在點O的正東方向選址建分校,考慮環境問題,要求校址到點O的距離大于4公里,并且鐵路上任意一點到校址的距離不能小于![]() 公里,求該校址距點O的最短距離(注:校址視為一個點)
公里,求該校址距點O的最短距離(注:校址視為一個點)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com