
分析 (Ⅰ)根據(jù)導(dǎo)數(shù)和幾何意義即可求出,
(Ⅱ)分離參數(shù),構(gòu)造函數(shù),利用導(dǎo)數(shù),求出函數(shù)的最值,即可求出參數(shù)的取值范圍
解答 解:(Ⅰ)∵f(x)=1+lnx-aex,
∴f′(x)=$\frac{1}{x}$-aex,x∈(0,+∞).
由于曲線y=f(x)在x=1處的切線與x軸平行,
∴f′(1)=1-ae=0,
解得$a=\frac{1}{e}$,
(Ⅱ)由條件知對任意x∈(0,+∞),不等式f(x)≤0恒成立,
此命題等價(jià)于a≥$\frac{1+lnx}{{e}^{x}}$對任意x∈(0,+∞)恒成立
令$h(x)=\frac{1+lnx}{e^x}$,x∈(0,+∞).
∴${h^'}(x)=\frac{{\frac{1}{x}-1-lnx}}{e^x}$=$\frac{1}{{e}^{x}}$($\frac{1}{x}$-1-lnx),x∈(0,+∞).
令g(x)=($\frac{1}{x}$-1-lnx),x∈(0,+∞).
則g′(x)=-$\frac{1}{{x}^{2}}$-$\frac{1}{x}$<0.
∴函數(shù)g(x)在x∈(0,+∞)上單調(diào)遞減.
注意到g(1)=0,即x=1是g(x)的零點(diǎn),
而當(dāng)x∈(0,1)時(shí),g(x)>0;當(dāng)x∈(1,+∞)時(shí),g(x)<0.
又ex>0,所以當(dāng)∈(0,1)時(shí),h′(x)>0;當(dāng)x∈(1,+∞)時(shí),h′(x)<0.
則當(dāng)x變化時(shí),h′(x)的變化情況如下表:
| x | (0,1) | 1 | (1,+∞) |
| h′(x) | + | 0 | - |
| h(x) | ↗ | 極大值$\frac{1}{e}$ | ↘ |
點(diǎn)評(píng) 本題考查利用函數(shù)的最值求參數(shù)問題,解題時(shí)要認(rèn)真審題,仔細(xì)解答,考查了等價(jià)轉(zhuǎn)化思想及導(dǎo)數(shù)性質(zhì)的合理運(yùn)用,屬于難題



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 18 | B. | 20 | C. | 24 | D. | 26 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
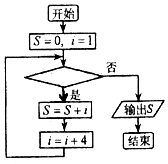
| A. | i≤504 | B. | i≤2009 | C. | i≤2013 | D. | i<2013 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 3 | B. | 3$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | $\frac{3\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | -$\frac{7}{5}$ | B. | -$\frac{1}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{7}{5}$ |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com