
分析 (1)先分別求出普通方程,再寫出極坐標方程;
(2)利用極徑的意義,即可得出結論.
解答 解:(1)圓C1和C2的參數方程分別是$\left\{\begin{array}{l}x=2+2cosϕ\\ y=2sinϕ\end{array}\right.$(ϕ為參數)和$\left\{\begin{array}{l}x=cosβ\\ y=1+sinβ\end{array}\right.$(β為參數),
普通方程分別為(x-2)2+y2=4,x2+(y-1)2=1,極坐標方程分別為ρ=4cosθ,ρ=2sinθ;
(2)設P,Q對應的極徑分別為ρ1,ρ2,則|OP|•|OQ|=ρ1ρ2=4sin2α,
∴sin2α=1,|OP|•|OQ|的最大值為4.
點評 本題考查三種方程的轉化,考查極徑的意義的運用,屬于中檔題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\frac{{\sqrt{7}}}{2}$ | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | y=-1 | B. | y=1 | C. | x=-$\frac{1}{16}$ | D. | x=$\frac{1}{16}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{13}+4\sqrt{5}$ | B. | $2+4\sqrt{5}$ | C. | $4+4\sqrt{5}$ | D. | $6\sqrt{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 在四棱錐P-ABCE中,PA⊥底面ABCE,CD⊥AE,AC平分∠BAD,G為PC的中點,PA=AD=2,BC=DE,AB=3,CD=2$\sqrt{3}$,F,M分別為BC,EG上一點,且AF∥CD.
在四棱錐P-ABCE中,PA⊥底面ABCE,CD⊥AE,AC平分∠BAD,G為PC的中點,PA=AD=2,BC=DE,AB=3,CD=2$\sqrt{3}$,F,M分別為BC,EG上一點,且AF∥CD.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
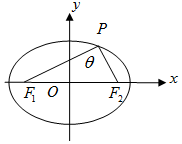 橢圓$\frac{x^2}{4}+{y^2}$=1上的一點P與兩焦點F1,F2所構成的三角形稱為焦點三角形.
橢圓$\frac{x^2}{4}+{y^2}$=1上的一點P與兩焦點F1,F2所構成的三角形稱為焦點三角形.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com