
【題目】選修4-4:坐標系與參數方程
已知曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),設直線
為參數),設直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)將曲線![]() 的參數方程化為普通方程,并指出其曲線是什么曲線;
的參數方程化為普通方程,并指出其曲線是什么曲線;
(2)設直線![]() 與
與![]() 軸的交點為
軸的交點為![]() 為曲線
為曲線![]() 上一動點,求
上一動點,求![]() 的最大值.
的最大值.
 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】經過長期觀測得到:在交通繁忙的時段內,某公路汽車的車流量![]() (千輛/h)與汽車的平均速度
(千輛/h)與汽車的平均速度![]() 之間的函數關系式為:
之間的函數關系式為:![]() .
.
(1)若要求在該段時間內車流量超過2千輛![]() ,則汽車在平均速度應在什么范圍內?
,則汽車在平均速度應在什么范圍內?
(2)在該時段內,若規定汽車平均速度不得超過![]() ,當汽車的平均速度
,當汽車的平均速度![]() 為多少時,車流量最大?最大車流量為多少?
為多少時,車流量最大?最大車流量為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國是世界上嚴重缺水的國家,某市政府為了鼓勵居民節約用水,計劃調整居民生活用水收費方案,擬確定一個合理的月用水量標準![]() (噸)、一位居民的月用水量不超過
(噸)、一位居民的月用水量不超過![]() 的部分按平價收費,超出
的部分按平價收費,超出![]() 的部分按議價收費.為了了解居民用水情況,通過抽樣,獲得了某年100位居民每人的月均用水量(單位:噸),將數據按照[0,0.5),[0.5,1),…,[4,4.5]分成9組,制成了如圖所示的頻率分布直方圖.
的部分按議價收費.為了了解居民用水情況,通過抽樣,獲得了某年100位居民每人的月均用水量(單位:噸),將數據按照[0,0.5),[0.5,1),…,[4,4.5]分成9組,制成了如圖所示的頻率分布直方圖.

(Ⅰ)求直方圖中a的值;
(Ⅱ)設該市有30萬居民,估計全市居民中月均用水量不低于3噸的人數,并說明理由;
(Ⅲ)若該市政府希望使85%的居民每月的用水量不超過標準![]() (噸),估計
(噸),估計![]() 的值,并說明理由.
的值,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)是R上的奇函數,當x>0時,解析式為f(x)=![]() .
.
(1)求f(x)在R上的解析式;
(2)用定義證明f(x)在(0,+∞)上為減函數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}滿足:an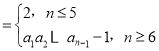 (n∈N*).若正整數k(k≥5)使得a12+a22+…+ak2=a1a2…ak成立,則k=( )
(n∈N*).若正整數k(k≥5)使得a12+a22+…+ak2=a1a2…ak成立,則k=( )
A.16B.17C.18D.19
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線![]() 的離心率為2,過點
的離心率為2,過點![]() 、斜率為1的直線
、斜率為1的直線![]() 與雙曲線
與雙曲線![]() 交于
交于![]() 、
、![]() 兩點且
兩點且![]() ,
,![]() .
.
(1)求雙曲線方程。
(2)設![]() 為雙曲線
為雙曲線![]() 右支上動點,
右支上動點,![]() 為雙曲線
為雙曲線![]() 的右焦點,在
的右焦點,在![]() 軸負半軸上是否存在定點
軸負半軸上是否存在定點![]() ,使得
,使得![]() ?若存在,求出點
?若存在,求出點![]() 的坐標;若不存在,請說明理由。
的坐標;若不存在,請說明理由。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com