
分析 (Ⅰ)根據奇函數的定義求解即可;
( II)根據奇函數的性質,不等式可轉化為f(x2+x)<f(4-2x),對a進行分類討論,由函數的單調性分別求解即可;
(III)由f(1)=$\frac{8}{3}$,求出a=3,不等式可轉化為32x+3-2x-2m•(3x-3-x)+2>0恒成立,構造函數令t=3x-3-x,t>$\frac{8}{3}$,得出2m<t+$\frac{4}{t}$,只需求出右式的最小值即可.
解答 解:(Ⅰ)由函數f(x)為R上的奇函數,
則f(0)=0,得k-1=0,解得k=1;
( II)由(Ⅰ)得:f(x)=ax-a-x,
不等式f(x2+x)+f(2x-4)<0,
即f(x2+x)<f(4-2x)
當a>1時,f(x)遞增,故x2+x<4-2x,
解得:-4<x<1,
故不等式的解集是(-4,1);
當1>a>0時,f(x)遞減,故x2+x>4-2x,
解得:x>1或x<-4,
故不等式的解集是:(-∞,-4)∪(1,+∞);
(III)又∵f(1)=$\frac{8}{3}$,即a-a-1=$\frac{8}{3}$,解得a=-$\frac{1}{3}$(舍去)或a=3,
∴f(x)=3x-3-x,
g(x)=a2x+a-2x-2m•f(x)+2在[1,+∞)恒為正,
∴32x+3-2x-2m•(3x-3-x)+2>0恒成立,
令t=3x-3-x,則t≥$\frac{8}{3}$,
∴2m<t+$\frac{4}{t}$,
顯然可知t+$\frac{4}{t}$的最小值為$\frac{25}{6}$,
∴$m∈(-∞,\frac{25}{12})$.
點評 本題考查了奇函數的概念和應用,利用構造函數的方法把恒成立問題轉化為求函數最值問題.


 教材全解字詞句篇系列答案
教材全解字詞句篇系列答案科目:高中數學 來源: 題型:選擇題
| A. | (-1,1) | B. | [-1,1] | C. | (-∞,-1]∪[1,+∞) | D. | (-∞,-1)∪(1,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
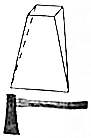 斧頭的形狀叫楔形,在《算數書》中又稱之為“鄆(y$\stackrel{、}{u}$n)都”或“壍(qi$\stackrel{、}{a}$n)堵”:其上底是一矩形,下底是一線段.有一斧頭:上厚為三,下厚為六,高為五及袤(m$\stackrel{、}{a}$o)為二,問此斧頭的體積為幾何?意思就是說有一斧頭形的幾何體,上底為矩形,下底為一線段,上底的長為3,下底線段長為6,上下底間的距離(高)為5,上底矩形的寬為2,則此幾何體的體積是( )
斧頭的形狀叫楔形,在《算數書》中又稱之為“鄆(y$\stackrel{、}{u}$n)都”或“壍(qi$\stackrel{、}{a}$n)堵”:其上底是一矩形,下底是一線段.有一斧頭:上厚為三,下厚為六,高為五及袤(m$\stackrel{、}{a}$o)為二,問此斧頭的體積為幾何?意思就是說有一斧頭形的幾何體,上底為矩形,下底為一線段,上底的長為3,下底線段長為6,上下底間的距離(高)為5,上底矩形的寬為2,則此幾何體的體積是( )| A. | 6 | B. | 10 | C. | 16 | D. | 20 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com