
已知函數 (
( R),
R), 為其導函數,且
為其導函數,且 時
時 有極小值
有極小值 .
.
(1)求 的單調遞減區(qū)間;
的單調遞減區(qū)間;
(2)若 ,
, ,當
,當 時,對于任意x,
時,對于任意x, 和
和 的值至少有一個是正數,求實數m的取值范圍;
的值至少有一個是正數,求實數m的取值范圍;
(3)若不等式 (
( 為正整數)對任意正實數
為正整數)對任意正實數 恒成立,求
恒成立,求 的最大值.
的最大值.
(1) ;(2)
;(2)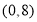 ;(3)6.
;(3)6.
【解析】
試題分析:(1)首先要求得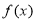 的解析式,其中有兩個參數
的解析式,其中有兩個參數 ,已知條件告訴我們
,已知條件告訴我們 以及
以及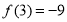 ,由此我們把這兩個等式表示出來就可解得
,由此我們把這兩個等式表示出來就可解得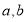 ,然后解不等式
,然后解不等式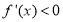 即可得遞減區(qū)間;(2)由(1)可得
即可得遞減區(qū)間;(2)由(1)可得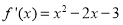 ,
,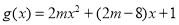 ,由于
,由于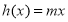 ,又
,又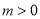 ,當
,當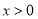 時,
時,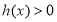 ,因此此時已符合題意,當
,因此此時已符合題意,當 時,
時,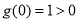 也符合題意,而當
也符合題意,而當 時,
時, ,因此我們只要求此時
,因此我們只要求此時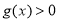 ,
,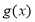 是二次函數,圖象是開口方向向上的拋物線,故可采用分類討論方法求得
是二次函數,圖象是開口方向向上的拋物線,故可采用分類討論方法求得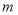 的范圍,使
的范圍,使 ;(3)不等式
;(3)不等式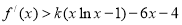 為
為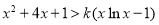 ,即
,即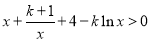 ,設
,設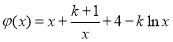 ,由
,由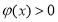 恒成立,只要
恒成立,只要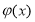 的最小值大于0即可,下面就是求
的最小值大于0即可,下面就是求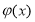 的最小值,同樣利用導函數
的最小值,同樣利用導函數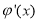 可求得
可求得 ,于是只要
,于是只要 ,變形為
,變形為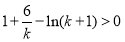 ,作為
,作為 的函數
的函數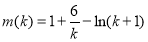 ,可證明它在
,可證明它在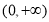 上是減函數,又
上是減函數,又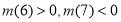 ,故可得
,故可得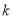 的最大值為6.
的最大值為6.
(1)由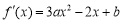 ,因為函數在
,因為函數在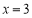 時有極小值
時有極小值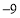 ,
,
所以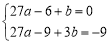 ,從而得
,從而得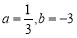 , 2分
, 2分
所求的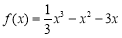 ,所以
,所以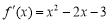 ,
,
由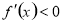 解得
解得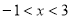 ,
,
所以 的單調遞減區(qū)間為
的單調遞減區(qū)間為 , 4分
, 4分
(2)由 ,故
,故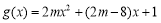 ,
,
當m>0時,若x>0,則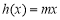 >0,滿足條件; 5分
>0,滿足條件; 5分
若x=0,則 >0,滿足條件; 6分
>0,滿足條件; 6分
若x<0,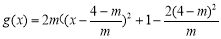
①如果對稱軸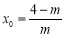 ≥0,即0<m≤4時,
≥0,即0<m≤4時,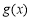 的開口向上,
的開口向上,
故在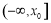 上單調遞減,又
上單調遞減,又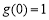 ,所以當x<0時,
,所以當x<0時,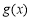 >0 8分
>0 8分
②如果對稱軸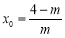 <0,即4<m時,
<0,即4<m時,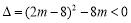
解得2<m<8,故4<m <8時, >0;
>0;
所以m的取值范圍為(0,8); 10分
(3)因為 ,所以
,所以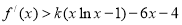 等價于
等價于
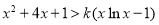 ,即
,即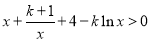 ,
,
記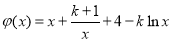 ,則
,則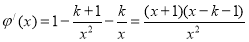 ,
,
由 ,得
,得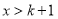 ,
,
所以 在
在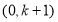 上單調遞減,在
上單調遞減,在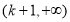 上單調遞增,
上單調遞增,
所以 , 12分
, 12分
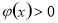 對任意正實數
對任意正實數 恒成立,等價于
恒成立,等價于 ,即
,即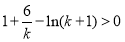 ,
,
記 ,則
,則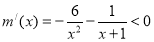 ,
,
所以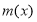 在
在 上單調遞減,又
上單調遞減,又 ,
,
所以 的最大值為
的最大值為 . 16分
. 16分
考點:(1)函數的極值,單調區(qū)間;(2)分類討論;(3)不等式恒成立與函數的最值及函數的單調性.


科目:高中數學 來源:2013-2014學年江蘇省蘇、錫、常、鎮(zhèn)四市高三教學情況調查(一)理科數學試卷(解析版) 題型:解答題
如圖,在平面直角坐標系 中,已知
中,已知 ,
, ,
, 是橢圓
是橢圓 上不同的三點,
上不同的三點, ,
, ,
, 在第三象限,線段
在第三象限,線段 的中點在直線
的中點在直線 上.
上.

(1)求橢圓的標準方程;
(2)求點C的坐標;
(3)設動點 在橢圓上(異于點
在橢圓上(異于點 ,
, ,
, )且直線PB,PC分別交直線OA于
)且直線PB,PC分別交直線OA于 ,
, 兩點,證明
兩點,證明 為定值并求出該定值.
為定值并求出該定值.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年江蘇省鹽城市高三第三次模擬考試數學試卷(解析版) 題型:解答題
已知曲線 的參數方程為
的參數方程為 (
(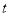 為參數),曲線
為參數),曲線 在點
在點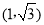 處的切線為
處的切線為 .以坐標原點為極點,
.以坐標原點為極點, 軸的正半軸為極軸建立極坐標系,求
軸的正半軸為極軸建立極坐標系,求 的極坐標方程.
的極坐標方程.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年江蘇省淮安市高三5月信息卷理科數學試卷(解析版) 題型:解答題
某超市在節(jié)日期間進行有獎促銷,規(guī)定凡在該超市購物滿400元的顧客,均可獲得一次摸獎機會.摸獎規(guī)則如下:
獎盒中放有除顏色不同外其余完全相同的4個球(紅、黃、黑、白).顧客不放回的每次摸出1個球,若摸到黑球則摸獎停止,否則就繼續(xù)摸球.按規(guī)定摸到紅球獎勵20元,摸到白球或黃球獎勵10元,摸到黑球不獎勵.
(1)求1名顧客摸球2次摸獎停止的概率;
(2)記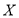 為1名顧客摸獎獲得的獎金數額,求隨機變量
為1名顧客摸獎獲得的獎金數額,求隨機變量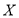 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年江蘇省淮安市高三5月信息卷理科數學試卷(解析版) 題型:解答題
在△ABC中,內角A,B,C的對邊分別為a,b,c,若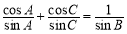 .
.
(1)求證: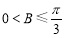 ;
;
(2)若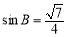 ,且
,且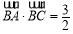 ,求
,求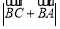 的值.
的值.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年江蘇省淮安市高三Ⅲ級部決戰(zhàn)四統測二文科數學試卷(解析版) 題型:填空題
設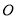 為坐標原點,給定一個定點
為坐標原點,給定一個定點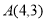 ,而點
,而點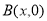 在
在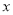 正半軸上移動,
正半軸上移動,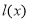 表示
表示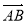 的長,則
的長,則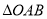 中兩邊長的比值
中兩邊長的比值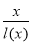 的最大值為 .
的最大值為 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com