
如圖,在平面直角坐標系 中,已知
中,已知 ,
, ,
, 是橢圓
是橢圓 上不同的三點,
上不同的三點, ,
, ,
, 在第三象限,線段
在第三象限,線段 的中點在直線
的中點在直線 上.
上.

(1)求橢圓的標準方程;
(2)求點C的坐標;
(3)設動點 在橢圓上(異于點
在橢圓上(異于點 ,
, ,
, )且直線PB,PC分別交直線OA于
)且直線PB,PC分別交直線OA于 ,
, 兩點,證明
兩點,證明 為定值并求出該定值.
為定值并求出該定值.
(1)求橢圓方程一般用待定系數法.本題已知橢圓過兩點,列兩個方程 ,解出
,解出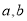 的值,(2)求點
的值,(2)求點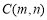 的坐標,需列出兩個方程.一是點C在橢圓上,即
的坐標,需列出兩個方程.一是點C在橢圓上,即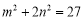 ,二是
,二是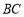 的中點在直線
的中點在直線 上,即
上,即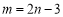 .注意到
.注意到 在第三象限,舍去正值.(3)題意明確,思路簡潔,就是求出點
在第三象限,舍去正值.(3)題意明確,思路簡潔,就是求出點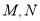 的坐標,算出
的坐標,算出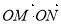 為定值.難點是如何消去參數.因為點
為定值.難點是如何消去參數.因為點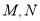 在直線
在直線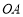 :
: 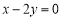 上,所以可設
上,所以可設 ,
,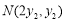 .選擇
.選擇 作為參數,即用
作為參數,即用 表示點
表示點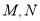 的坐標.由
的坐標.由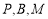 三點共線,解得
三點共線,解得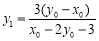 ,同理解得
,同理解得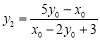 .從而有
.從而有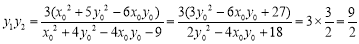 ,這里主要用到
,這里主要用到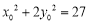 代入化簡.本題也可利用橢圓參數方程或三角表示揭示
代入化簡.本題也可利用橢圓參數方程或三角表示揭示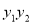 為定值.
為定值.
【解析】
試題分析:(1) ,(2)
,(2)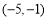 ,(3)
,(3)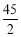 .
.
試題解析:(1)由已知,得 解得
解得 2分
2分
所以橢圓的標準方程為 . 3分
. 3分
(2)設點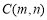
 ,則
,則 中點為
中點為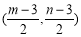 .
.
由已知,求得直線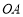 的方程為
的方程為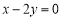 ,從而
,從而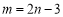 .①
.①
又∵點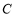 在橢圓上,∴
在橢圓上,∴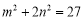 .②
.②
由①②,解得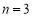 (舍),
(舍),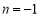 ,從而
,從而 . 5分
. 5分
所以點 的坐標為
的坐標為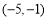 . 6分
. 6分
(3)設 ,
, ,
,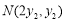 .
.
∵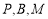 三點共線,∴
三點共線,∴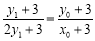 ,整理,得
,整理,得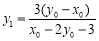 . 8分
. 8分
∵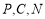 三點共線,∴
三點共線,∴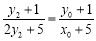 ,整理,得
,整理,得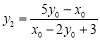 . 10分
. 10分
∵點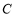 在橢圓上,∴
在橢圓上,∴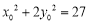 ,
,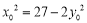 .
.
從而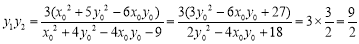 . 14分
. 14分
所以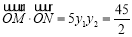 15分
15分
∴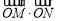 為定值,定值為
為定值,定值為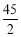 . 16分
. 16分
考點:橢圓標準方程,直線與橢圓位置關系


科目:高中數學 來源:2013-2014學年江蘇省連云港市高三3月第二次調研考試文科數學試卷(解析版) 題型:填空題
四棱錐P ? ABCD 的底面ABCD是邊長為2的正方形,PA⊥底面ABCD且PA = 4,則PC與底面ABCD所成角的正切值為 .
查看答案和解析>>
科目:高中數學 來源:2013-2014學年江蘇省蘇錫常鎮四市高三教學情況調研二數學試卷(解析版) 題型:填空題
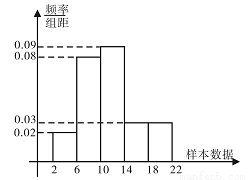
樣本容量為100的頻率分布直方圖如右圖所示,由此估計樣本數據落在[6,10]內的頻數為 .
查看答案和解析>>
科目:高中數學 來源:2013-2014學年江蘇省蘇、錫、常、鎮四市高三教學情況調查(一)理科數學試卷(解析版) 題型:解答題
在平面直角坐標系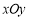 中,圓的參數方程為
中,圓的參數方程為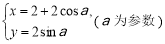 ,以坐標原點
,以坐標原點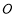 為極點,
為極點,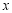 軸的正半軸為極軸建立極坐標系.求:
軸的正半軸為極軸建立極坐標系.求:
(1)圓的直角坐標方程;
(2)圓的極坐標方程.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年江蘇省蘇、錫、常、鎮四市高三教學情況調查(一)理科數學試卷(解析版) 題型:填空題
已知函數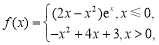
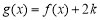 ,若函數
,若函數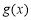 恰有兩個不同的零點,則實數
恰有兩個不同的零點,則實數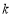 的取值范圍為 .
的取值范圍為 .
查看答案和解析>>
科目:高中數學 來源:2013-2014學年江蘇省淮安市高三5月信息卷理科數學試卷(解析版) 題型:解答題
已知函數 (
( R),
R), 為其導函數,且
為其導函數,且 時
時 有極小值
有極小值 .
.
(1)求 的單調遞減區間;
的單調遞減區間;
(2)若 ,
, ,當
,當 時,對于任意x,
時,對于任意x, 和
和 的值至少有一個是正數,求實數m的取值范圍;
的值至少有一個是正數,求實數m的取值范圍;
(3)若不等式 (
( 為正整數)對任意正實數
為正整數)對任意正實數 恒成立,求
恒成立,求 的最大值.
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com