
【題目】已知函數(shù)f(x)=(x2﹣x﹣1)ex .
(1)求函數(shù)f(x)的單調(diào)區(qū)間.
(2)若方程a( ![]() +1)+ex=ex在(0,1)內(nèi)有解,求實數(shù)a的取值范圍.
+1)+ex=ex在(0,1)內(nèi)有解,求實數(shù)a的取值范圍.
【答案】
(1)解: f′(x)=(x2+x﹣2)ex=(x﹣1)(x+2)ex,
令f′(x)>0,解得:x>1或x<﹣2,
令f′(x)<0,解得:﹣2<x<1,
故f(x)在(﹣∞,﹣2)遞增,在(﹣2,1)遞減,在(1,+∞)遞增;
(2)方程a( ![]() +1)+ex=ex可化為ex﹣ax2+(a﹣e)x=0,
+1)+ex=ex可化為ex﹣ax2+(a﹣e)x=0,
令g(x)=ex﹣ax2+(a﹣e)x,則g(x)在(0,1)內(nèi)有零點,易知g(0)=1,g(1)=0,
g′(x)=ex﹣2ax+a﹣e,設(shè)g′(x)=h(x),則h′(x)=ex﹣2a,
①a<0時,h′(x)>0,即h(x)在區(qū)間(0,1)遞增,h(0)=1+a﹣e<0,
h(1)=﹣a>0,即h(x)在區(qū)間(0,1)只有1個零點x1,
故g(x)在(0,x1)遞減,在(x1,1)遞增,
而g(0)=1>0,g(1)=0,得g(x1)<g(1)=0,故g(x)在(0,x1)內(nèi)存在唯一零點;
②當0≤a≤ ![]() 時,h′(x)>0,即h(x)在區(qū)間(0,1)遞增,
時,h′(x)>0,即h(x)在區(qū)間(0,1)遞增,
h(x)<h(1)=﹣a≤0,得g(x)在(0,1)遞減,得g(x)在(0,1)無零點;
③當 ![]() <a<
<a< ![]() 時,令h′(x)=0,得x=ln(2a)∈(0,1),
時,令h′(x)=0,得x=ln(2a)∈(0,1),
∴h(x)在區(qū)間(0,ln(2a))上遞減,在(ln(2a),1)遞增,
h(x)在區(qū)間(0,1)上存在最小值h(ln(2a)),
故h(ln(2a))<h(1)=﹣a<0,h(0)=1+a﹣e<a﹣ ![]() <0,
<0,
故 ![]() <a<
<a< ![]() 時,x∈(0,1),都有g(shù)′(x)<0,g(x)在(0,1)遞減,
時,x∈(0,1),都有g(shù)′(x)<0,g(x)在(0,1)遞減,
又g(0)=1,g(1)=0,故g(x)在(0,1)內(nèi)無零點;
④a≥ ![]() 時,h′(x)<0,h(x)在區(qū)間(0,1)遞減,h(1)=﹣a<0,h(0)=1+a﹣e,
時,h′(x)<0,h(x)在區(qū)間(0,1)遞減,h(1)=﹣a<0,h(0)=1+a﹣e,
若h(0)=1+a﹣e>0,得a>e﹣1> ![]() ,
,
則h(x)在區(qū)間(0,1)只有1個零點x2,
故g(x)在(0,x2)遞增,在(x2,1)遞減,
而g(0)=1,g(1)=0,得g(x)在(0,1)無零點,
若 ![]() <a時,則h(0)=1+a﹣e<0,得g(x)在(0,1)遞減,得g(x)在(0,1)內(nèi)無零點,
<a時,則h(0)=1+a﹣e<0,得g(x)在(0,1)遞減,得g(x)在(0,1)內(nèi)無零點,
綜上,a<0時,方程a( ![]() +1)+ex=ex在(0,1)內(nèi)有解.
+1)+ex=ex在(0,1)內(nèi)有解.
【解析】(1)對f(x)求導,討論函數(shù)的單調(diào)區(qū)間即可,(2)問題可化為ex﹣ax2+(a﹣e)x=0,令g(x)=ex﹣ax2+(a﹣e)x,則g(x)在(0,1)內(nèi)由零點,討論a的范圍,求出函數(shù)的單調(diào)區(qū)間,從而確定a的范圍即可.
【考點精析】掌握利用導數(shù)研究函數(shù)的單調(diào)性和函數(shù)的極值與導數(shù)是解答本題的根本,需要知道一般的,函數(shù)的單調(diào)性與其導數(shù)的正負有如下關(guān)系: 在某個區(qū)間![]() 內(nèi),(1)如果
內(nèi),(1)如果![]() ,那么函數(shù)
,那么函數(shù)![]() 在這個區(qū)間單調(diào)遞增;(2)如果
在這個區(qū)間單調(diào)遞增;(2)如果![]() ,那么函數(shù)
,那么函數(shù)![]() 在這個區(qū)間單調(diào)遞減;求函數(shù)
在這個區(qū)間單調(diào)遞減;求函數(shù)![]() 的極值的方法是:(1)如果在
的極值的方法是:(1)如果在![]() 附近的左側(cè)
附近的左側(cè)![]() ,右側(cè)
,右側(cè)![]() ,那么
,那么![]() 是極大值(2)如果在
是極大值(2)如果在![]() 附近的左側(cè)
附近的左側(cè)![]() ,右側(cè)
,右側(cè)![]() ,那么
,那么![]() 是極小值.
是極小值.


科目:高中數(shù)學 來源: 題型:
【題目】已知非零平面向量 ![]() ,
, ![]() ,則“|
,則“| ![]() |=|
|=| ![]() |+|
|+| ![]() |”是“存在非零實數(shù)λ,使
|”是“存在非零實數(shù)λ,使 ![]() =λ
=λ ![]() ”的( )
”的( )
A.充分而不必要條件
B.必要而不充分條件
C.充分必要條件
D.既不充分也不必要條件
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在三棱錐P﹣ABC中,平面PAC⊥平面ABC,PA⊥AC,AB⊥BC.設(shè)D,E分別為PA,AC中點.
(Ⅰ)求證:DE∥平面PBC;
(Ⅱ)求證:BC⊥平面PAB;
(Ⅲ)試問在線段AB上是否存在點F,使得過三點 D,E,F(xiàn)的平面內(nèi)的任一條直線都與平面PBC平行?若存在,指出點F的位置并證明;若不存在,請說明理由.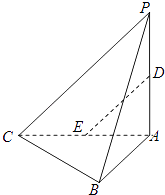
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】經(jīng)銷商經(jīng)銷某種農(nóng)產(chǎn)品,在一個銷售季度內(nèi),每售出1t該產(chǎn)品獲利潤500元,未售出的產(chǎn)品,每1t虧損300元.根據(jù)歷史資料,得到銷售季度內(nèi)市場需求量的頻率分布直方圖,如圖所示.經(jīng)銷商為下一個銷售季度購進了130t該農(nóng)產(chǎn)品.以X(單位:t,100≤X≤150)表示下一個銷售季度內(nèi)的市場需求量,T(單位:元)表示下一個銷售季度內(nèi)經(jīng)銷該農(nóng)產(chǎn)品的利潤.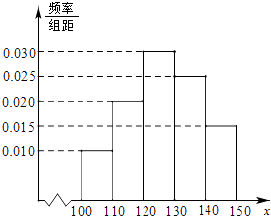
(Ⅰ)將T表示為X的函數(shù);
(Ⅱ)根據(jù)直方圖估計利潤T不少于57000元的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知實數(shù)x,y滿足不等式組  ,若目標函數(shù)z=kx+y僅在點(1,1)處取得最小值,則實數(shù)k的取值范圍是 ( )
,若目標函數(shù)z=kx+y僅在點(1,1)處取得最小值,則實數(shù)k的取值范圍是 ( )
A.(﹣1,+∞)
B.(﹣∞,﹣1)
C.(1,+∞)
D.(﹣∞,1)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)=(x2+ax+b)ex , 當b<1時,函數(shù)f(x)在(﹣∞,﹣2),(1,+∞)上均為增函數(shù),則 ![]() 的取值范圍是 .
的取值范圍是 .
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)=log2(|x﹣1|+|x+2|﹣a).
(Ⅰ)當a=7時,求函數(shù)f(x)的定義域;
(Ⅱ)若關(guān)于x的不等式f(x)≥3的解集是R,求實數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù) ![]() ,且f(1)=1,f(﹣2)=4.
,且f(1)=1,f(﹣2)=4.
(1)求a、b的值;
(2)已知定點A(1,0),設(shè)點P(x,y)是函數(shù)y=f(x)(x<﹣1)圖象上的任意一點,求|AP|的最小值,并求此時點P的坐標;
(3)當x∈[1,2]時,不等式 ![]() 恒成立,求實數(shù)m的取值范圍.
恒成立,求實數(shù)m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,橢圓E: ![]() =1(a>b>0)的左頂點為A(﹣2,0),離心率為
=1(a>b>0)的左頂點為A(﹣2,0),離心率為 ![]() ,過點A的直線l與橢圓E交于另一點B,點C為y軸上的一點.
,過點A的直線l與橢圓E交于另一點B,點C為y軸上的一點.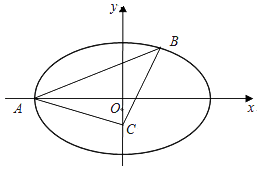
(1)求橢圓E的標準方程;
(2)若△ABC是以點C為直角頂點的等腰直角三角形,求直線l的方程.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com