
【題目】如圖,在三棱錐P﹣ABC中,平面PAC⊥平面ABC,PA⊥AC,AB⊥BC.設D,E分別為PA,AC中點.
(Ⅰ)求證:DE∥平面PBC;
(Ⅱ)求證:BC⊥平面PAB;
(Ⅲ)試問在線段AB上是否存在點F,使得過三點 D,E,F的平面內的任一條直線都與平面PBC平行?若存在,指出點F的位置并證明;若不存在,請說明理由.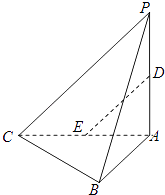
【答案】解:(Ⅰ)證明:因為點E是AC中點,點D為PA的中點,所以DE∥PC.
又因為DE面PBC,PC面PBC,
所以DE∥平面PBC.
(Ⅱ)證明:因為平面PAC⊥面ABC,平面PAC∩平面ABC=AC,又PA平面PAC,PA⊥AC,
所以PA⊥面ABC,
因為BC平面ABC,
所以PA⊥BC.
又因為AB⊥BC,且PA∩AB=A,
所以BC⊥面PAB.
(Ⅲ)解:當點F是線段AB中點時,過點D,E,F的平面內的任一條直線都與平面PBC平行.
取AB中點F,連EF,連DF.
由(Ⅰ)可知DE∥平面PBC.
因為點E是AC中點,點F為AB的中點,
所以EF∥BC.
又因為EF平面PBC,BC平面PBC,
所以EF∥平面PBC.
又因為DE∩EF=E,
所以平面DEF∥平面PBC,
所以平面DEF內的任一條直線都與平面PBC平行.
故當點F是線段AB中點時,過點D,E,F所在平面內的任一條直線都與平面PBC平行.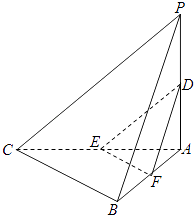
【解析】(Ⅰ)證明以DE∥平面PBC,只需證明DE∥PC;(Ⅱ)證明BC⊥平面PAB,根據線面垂直的判定定理,只需證明PA⊥BC,AB⊥BC;(Ⅲ)當點F是線段AB中點時,證明平面DEF∥平面PBC,可得平面DEF內的任一條直線都與平面PBC平行.
【考點精析】本題主要考查了直線與平面平行的判定和直線與平面平行的性質的相關知識點,需要掌握平面外一條直線與此平面內的一條直線平行,則該直線與此平面平行;簡記為:線線平行,則線面平行;一條直線與一個平面平行,則過這條直線的任一平面與此平面的交線與該直線平行;簡記為:線面平行則線線平行才能正確解答此題.


 挑戰100單元檢測試卷系列答案
挑戰100單元檢測試卷系列答案科目:高中數學 來源: 題型:
【題目】已知△ABC滿足| ![]() |=3,|
|=3,| ![]() |=4,O是△ABC所在平面內一點,滿足|
|=4,O是△ABC所在平面內一點,滿足| ![]() |=|
|=| ![]() |=|
|=| ![]() |,且
|,且 ![]() =λ
=λ ![]() +
+ ![]()
![]() (λ∈R),則cos∠BAC= .
(λ∈R),則cos∠BAC= .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】學校藝術節對同一類的![]() ,
,![]() ,
,![]() ,
,![]() 四項參賽作品,只評一項一等獎,在評獎揭曉前,甲、乙、丙、丁四位同學對這四項參賽作品預測如下:
四項參賽作品,只評一項一等獎,在評獎揭曉前,甲、乙、丙、丁四位同學對這四項參賽作品預測如下:
甲說:“是![]() 或
或![]() 作品獲得一等獎”;
作品獲得一等獎”;
乙說:“![]() 作品獲得一等獎”;
作品獲得一等獎”;
丙說:“![]() ,
,![]() 兩項作品未獲得一等獎”;
兩項作品未獲得一等獎”;
丁說:“是![]() 作品獲得一等獎”.
作品獲得一等獎”.
若這四位同學中只有兩位說的話是對的,則獲得一等獎的作品是__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正方形ABCD和四邊形ACEF所在的平面互相垂直.EF∥AC,AB= ![]() ,CE=EF=1. (Ⅰ)求證:AF∥平面BDE;
,CE=EF=1. (Ⅰ)求證:AF∥平面BDE;
(Ⅱ)求證:CF⊥平面BDE.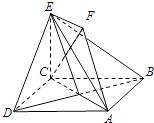
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】小明同學在寒假社會實踐活動中,對白天平均氣溫與某家奶茶店的![]() 品牌飲料銷量之間的關系進行了分析研究,他分別記錄了1月11日至1月15日的白天氣溫
品牌飲料銷量之間的關系進行了分析研究,他分別記錄了1月11日至1月15日的白天氣溫![]() (
(![]() )與該奶茶店的
)與該奶茶店的![]() 品牌飲料銷量
品牌飲料銷量![]() (杯),得到如表數據:
(杯),得到如表數據:
日期 | 1月11號 | 1月12號 | 1月13號 | 1月14號 | 1月15號 |
平均氣溫 | 9 | 10 | 12 | 11 | 8 |
銷量 | 23 | 25 | 30 | 26 | 21 |
(1)若先從這五組數據中抽出2組,求抽出的2組數據恰好是相鄰2天數據的概率;
(2)請根據所給五組數據,求出![]() 關于
關于![]() 的線性回歸方程式
的線性回歸方程式![]() ;
;
(3)根據(2)所得的線性回歸方程,若天氣預報1月16號的白天平均氣溫為![]() ,請預測該奶茶店這種飲料的銷量.
,請預測該奶茶店這種飲料的銷量.
(參考公式: ,
,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數 ![]() .
.
(1)證明f(x)在(0,+∞)上單調遞增;
(2)是否存在實數a使得f(x)的定義域、值域都是 ![]() ,若存在求出a的值,若不存在說明理由.
,若存在求出a的值,若不存在說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
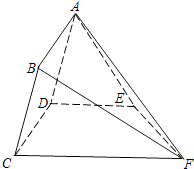
【題目】如圖,矩形ABCD所在的半平面和直角梯形CDEF所在的半平面成60°的二面角,DE∥CF,CD⊥DE,AD=2, ![]() ,CF=6,∠CFE=45°.
,CF=6,∠CFE=45°.
(Ⅰ)求證:BF∥平面ADE;
(Ⅱ)在線段CF上求一點G,使銳二面角B﹣EG﹣D的余弦值為 ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐P﹣ABCD底面是正方形,PA⊥底面ABCD,E,F分別為PA,PD中點. 
(1)求證:EF∥面PBC
(2)求證:平面PBC⊥平面PAB.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com