
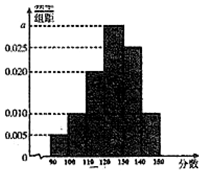
 某高校從2016年招收的大一新生中,隨機抽取60名學生,將他們的2016年高考數學成績(滿分150分,成績均不低于90分的整數)分成六段[90,100),[100,110)…[140,150),后得到如圖所示的頻率分布直方圖.
某高校從2016年招收的大一新生中,隨機抽取60名學生,將他們的2016年高考數學成績(滿分150分,成績均不低于90分的整數)分成六段[90,100),[100,110)…[140,150),后得到如圖所示的頻率分布直方圖.分析 (1)由頻率分布直方圖能求出a的值.
(2)由頻率分布直方圖能估計該校招收的大一新生2016年高考數學成績不低于120分的人數.
(3)用分層抽樣的方法從數學成績在[90,100)與[140,150]兩個分數段內的學生中抽取一個容量為6的樣本,則數學成績在[90,100)分數段內的學生抽取2人,數學成績在[140,150]分數段內的學生抽取4人,至少有1人在分數段[90,100)內的對立事件是抽到的2人都在分數段[140,150]內,由此利用對立事件概率計算公式能求出至少有1人在分數段[90,100)內的概率.
解答 解:(1)由頻率分布直方圖得:
(0.005+0.01×2+0.02+0.025+a)×10=1,解得a=0.03(2分)
(2)由頻率分布直方圖估計該校招收的大一新生2015年高考數學成績不低于1(20分)的人數為:(0.03+0.025+0.01)×10×960=624(人).(4分)
(3)用分層抽樣的方法從數學成績在[90,100)與[140,150]兩個分數段內的學生中抽取一個容量為6的樣本,
∵數學成績在[90,100)分數段內的學生頻率為0.005×10=0.05,
數學成績在[140,150]分數段內的學生頻率為0.010×10=0.10,
∴數學成績在[90,100)分數段內的學生抽取2人,數學成績在[140,150]分數段內的學生抽取4人,
∴將該樣本看成一個總體,從中任取2人,基本事件總數n=15,
至少有1人在分數段[90,100)內的對立事件是抽到的2人都在分數段[140,150]內,
∴至少有1人在分數段[90,100)內的概率:P=$\frac{3}{5}$.(12分)
點評 本題考查頻率分布直方圖的應用,考查概率的求法,是基礎題,解題時要認真審題,注意對立事件概率計算公式的合理運用.


科目:高中數學 來源: 題型:選擇題
| A. | 4+$\sqrt{5}$ | B. | 4-$\sqrt{5}$ | C. | 2 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
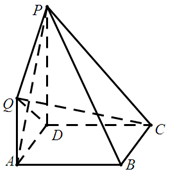 如圖,四邊形ABCD為正方形,PD⊥平面ABCD,PD∥QA,$QA=AB=\frac{1}{2}PD$.
如圖,四邊形ABCD為正方形,PD⊥平面ABCD,PD∥QA,$QA=AB=\frac{1}{2}PD$.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com