Question

12．在極坐標系中，已知圓C的圓心C（3，$\frac{π}{9}$），半徑為1．Q點在圓周上運動，O為極點．
（1）求圓C的極坐標方程；
（2）若P在直線OQ上運動，且滿足$\frac{OQ}{QP}$=$\frac{2}{3}$，求動點P的軌跡方程．

Answer 1

分析 （1）設M（ρ，θ）為圓C上任意一點，由余弦定理，得1=ρ²+9-2•ρ•3•cos（$θ-\frac{π}{6}$），由此能求出圓C的軌跡方程．
（2）設Q（ρ₁，θ₁），則${{ρ}_{1}}^{2}$-6•ρ₁cos（${θ}_{1}-\frac{π}{6}$）+8=0，設P（ρ，θ），則OQ：QP=ρ₁：（ρ-ρ₁）=2：3，由此能求出P點的軌跡方程．

解答 解：（1）設M（ρ，θ）為圓C上任意一點，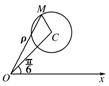
如圖，在△OCM中，|OC|=3，|OM|=ρ，|CM|=1，∠COM=|$θ-\frac{π}{6}$|，
根據余弦定理，得1=ρ²+9-2•ρ•3•cos（$θ-\frac{π}{6}$），
化簡整理，得ρ²-6•ρcos（$θ-\frac{π}{6}$）+8=0為圓C的極坐標方程．
（2）設Q（ρ₁，θ₁），
則有${{ρ}_{1}}^{2}$-6•ρ₁cos（${θ}_{1}-\frac{π}{6}$）+8=0，①
設P（ρ，θ），則OQ：QP=ρ₁：（ρ-ρ₁）=2：3，解得ρ₁=$\frac{2}{5}$ρ，
又θ₁=θ，即$\left\{\begin{array}{l}{{ρ}_{1}=\frac{2}{5}ρ}\\{{θ}_{1}=θ}\end{array}\right.$，
代入①得$\frac{4}{25}$ρ²-6•$\frac{2}{5}$ρcos（θ-$\frac{π}{6}$）+8=0，
整理得ρ²-15ρcos（$θ-\frac{5π}{6}$）+50=0為P點的軌跡方程．

點評 本題考查圓的極坐標方程的求法，考查點的軌跡坐標方程的求法，考查極坐標方程、直角坐標方程、參數方程的互化等基礎知識，考查推理論證能力、運算求解能力，考查化歸與轉化思想、函數與方程思想，是中檔題．