
分析 (1)求導數,利用函數f(x)=a•lnx+b•x2的圖象在點(1,f(1))處的切線方程為x-y-1=0,求出a,b,即可求f(x)的表達式;
(2)由題要證函數g(x)=2f(x+t),t∈R且t≤2,是函數h(x)=ex+f(x+t)的一個“游離承托函數”,只要證明當t≤2時,g(x)<h(x)在公共定義域上恒成立.
解答 (1)解:當x=1時,y=0,代入f(x)=a•lnx+b•x2得b=0,…(1分)
所以f(x)=a•lnx,f′(x)=$\frac{a}{x}$…(3分)
由切線方程知f′(1)=1,所以a=1,故f(x)=lnx.…(5分)
(2)證明:由題要證函數g(x)=2f(x+t),t∈R且t≤2,是函數h(x)=ex+f(x+t)的一個“游離承托函數”,
只要證明當t≤2時,g(x)<h(x)在公共定義域上恒成立,即證明:
當t≤2時,h(x)-g(x)=ex-ln(x+t)對于x>-t恒成立,
由于t≤2,x+t≤x+2,ln(x+t)≤ln(x+2),ex-ln(x+t)≥ex-ln(x+2),
只要證明:ex-ln(x+2)>0對于x>-2恒成立即可.…(6分)
證明:令y=ex-ln(x+2),x>-2,
則y′=ex-$\frac{1}{x+2}$,
令k(x)=ex-$\frac{1}{x+2}$,則k′(x)=ex+$\frac{1}{(x+2)^{2}}$>0,
∴y′=ex-$\frac{1}{x+2}$在(-2,+∞)上單調遞增,且k(-1)=$\frac{1}{e}$-1<0,k(0)=1-$\frac{1}{2}$>0
∴?x0∈(-1,0),使得k(x0)=0成立,…(8分)
當x∈(-2,x0)時,y′<0,y=ex-ln(x+2)單調遞減;
當x∈(x0,+∞)時,y′>0,y=ex-ln(x+2)單調遞增;
∴ymin=${e}^{{x}_{0}}$-ln(x0+2),…(9分)
又由k(x0)=0,得${e}^{{x}_{0}}$=$\frac{1}{{x}_{0}+2}$,且x0=-ln(x0+2)…(10分)
∴ymin=${e}^{{x}_{0}}$-ln(x0+2)=$\frac{({x}_{0}+1)^{2}}{{x}_{0}+2}$>0,…(11分)
∴ex-ln(x+2)>0對于x>-2恒成立
∴函數函數g(x)=2f(x+t),t∈R且t≤2,是函數h(x)=ex+f(x+t)的一個“游離承托函數”,得證.…(12分)
點評 本題主要考查了利用導數研究曲線上某點切線方程,以及函數恒成立問題等基礎題知識,考查運算求解能力,考查化歸與轉化思想,分類討論思想,屬于難題.


 周周清檢測系列答案
周周清檢測系列答案 輕巧奪冠周測月考直通高考系列答案
輕巧奪冠周測月考直通高考系列答案科目:高中數學 來源: 題型:解答題
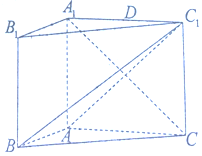 如圖,在三棱柱ABC-A1B1C1中,側面ABB1A1是矩形,∠BAC=90°,AA1⊥BC,AA1=AC=2AB=4,且BC1⊥A1C
如圖,在三棱柱ABC-A1B1C1中,側面ABB1A1是矩形,∠BAC=90°,AA1⊥BC,AA1=AC=2AB=4,且BC1⊥A1C查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{5}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | -$\sqrt{5}$ | D. | -$\frac{\sqrt{5}}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f(x)=x與g(x)=($\sqrt{x}$)2 | B. | f(x)=x|x|與g(x)=$\left\{\begin{array}{l}{{x}^{2}(x>0)}\\{-{x}^{2}(x<0)}\end{array}\right.$ | ||
| C. | f(x)=|x|與g(x)=$\root{3}{{x}^{3}}$ | D. | f(x)=$\frac{{x}^{2}-1}{x-1}$與g(t)=t+1(t≠1) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com