
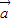 =(2cosα,2sinα),
=(2cosα,2sinα),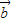 =(3cosβ,3sinβ),若向量
=(3cosβ,3sinβ),若向量 與
與 的夾角為60°,則直線
的夾角為60°,則直線 與圓
與圓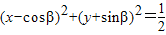 的位置關系是( )
的位置關系是( )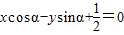 與圓
與圓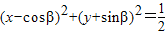 的方程,我們易得到圓心到直線距離d的表達式,再由向量
的方程,我們易得到圓心到直線距離d的表達式,再由向量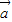 =(2cosα,2sinα),
=(2cosα,2sinα),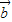 =(3cosβ,3sinβ),若向量
=(3cosβ,3sinβ),若向量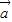 與
與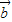 的夾角為60°,我們可以計算出d值,與圓半徑比較,即可得到答案.
的夾角為60°,我們可以計算出d值,與圓半徑比較,即可得到答案.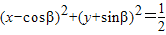
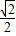
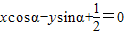 距離
距離 |=|cos(α-β)+
|=|cos(α-β)+ |
|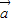 =(2cosα,2sinα),
=(2cosα,2sinα),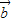 =(3cosβ,3sinβ),向量
=(3cosβ,3sinβ),向量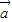 與
與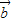 的夾角為60°,
的夾角為60°,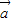 •
•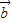 =6cosαcosβ+6sinαsinβ=2×3×
=6cosαcosβ+6sinαsinβ=2×3× =3
=3
 +
+ |=1>
|=1>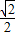 ,
,

 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中數學 來源: 題型:
| a |
| b |
| a |
| b |
| 1 |
| 2 |
| 1 |
| 2 |
| A、相交 | B、相切 |
| C、相離 | D、相交且過圓心 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| a |
| b |
| a |
| b |
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| OA |
| 2 |
| 2 |
| OB |
| π |
| 6 |
| π |
| 2 |
| 5π |
| 6 |
| a |
| b |
| a |
| a |
| b |
| a |
查看答案和解析>>
科目:高中數學 來源: 題型:
| m |
| n |
| m |
| n |
| π |
| 8 |
| 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com