
分析 (1)利用等比數列的公比,結合${S_4}=\frac{65}{24}$,直接求解a1;
(2)通過a1=2,化簡${c_n}=\frac{1}{2}{a_n}+bn$,利用c2,c4,c5成等差數列,得到方程,求解b即可.
解答 解:(1)∵公比$q=\frac{3}{2}$,${S_4}=\frac{65}{24}$,
∴$\frac{{{a_1}[1-{{(\frac{3}{2})}^4}]}}{{1-\frac{3}{2}}}=\frac{65}{24}$,
則$(1-\frac{81}{16}){a_1}=-\frac{65}{48}$,
解得${a_1}=\frac{1}{3}$.
(2)∵a1=2,公比為$\frac{3}{2}$,∴a2=3,${a_4}=\frac{27}{4}$,${a_5}=\frac{81}{8}$,
∴${c_2}=\frac{3}{2}+2b$,${c_4}=\frac{27}{8}+4b$,${c_5}=\frac{81}{16}+5b$.
∵c2,c4,c5成等差數列.
∴$2(\frac{27}{8}+4b)=\frac{3}{2}+2b+\frac{81}{16}+5b$.
解得$b=-\frac{3}{16}$.
點評 本題考查數列的遞推關系式的應用,考查轉化思想以及計算能力.


科目:高中數學 來源: 題型:解答題
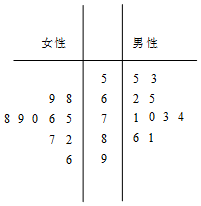 某城市為了滿足市民出行的需要和節能環保的要求,在公共場所提供單車共享服務,某部門為了對該城市共享單車進行監管,隨機選取了20位市民對共享單車的情況進行問卷調查,并根據其滿意度評分值(滿分100分)制作的莖葉圖如圖所示:
某城市為了滿足市民出行的需要和節能環保的要求,在公共場所提供單車共享服務,某部門為了對該城市共享單車進行監管,隨機選取了20位市民對共享單車的情況進行問卷調查,并根據其滿意度評分值(滿分100分)制作的莖葉圖如圖所示:查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $2+\sqrt{3}$ | B. | $2-\sqrt{3}$ | C. | $2+\sqrt{5}$ | D. | $\sqrt{5}-2$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 160 | B. | 180 | C. | 200 | D. | 220 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 喜愛 | 不喜愛 | 合計 | |
| 男同學 | 24 | 6 | 30 |
| 女同學 | 6 | 14 | 20 |
| 合計 | 30 | 20 | 50 |
| P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | g(x)可能沒有零點 | B. | g(x)可能有1個零點 | C. | g(x)可能有2個零點 | D. | g(x)可能有3個零點 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
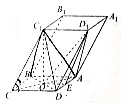 如圖所示,已知底面ABCD是正方形的四棱柱ABCD-A1B1C1D1,C1C=C1D,且∠C1CB=C1CD,線段AC與BD的交點為O.
如圖所示,已知底面ABCD是正方形的四棱柱ABCD-A1B1C1D1,C1C=C1D,且∠C1CB=C1CD,線段AC與BD的交點為O.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com