
| 連續劇播放時長(分鐘) | 廣告播放時長(分鐘) | 收視人次(萬) | |
| 甲 | 70 | 5 | 60 |
| 乙 | 60 | 5 | 25 |
分析 (Ⅰ)直接由題意結合圖表列關于x,y所滿足得不等式組,化簡后即可畫出二元一次不等式所表示的平面區域;
(Ⅱ)寫出總收視人次z=60x+25y.化目標函數為直線方程的斜截式,數形結合得到最優解,聯立方程組求得最優解的坐標,代入目標函數得答案.
解答 (Ⅰ)解:由已知,x,y滿足的數學關系式為$\left\{\begin{array}{l}70x+60y≤600\\ 5x+5y≥30\\ x≤2y\\ x≥0\\ y≥0\end{array}\right.$,即$\left\{\begin{array}{l}7x+6y≤60\\ x+y≥6\\ x-2y≤0\\ x≥0\\ y≥0\end{array}\right.$.
該二元一次不等式組所表示的平面區域如圖: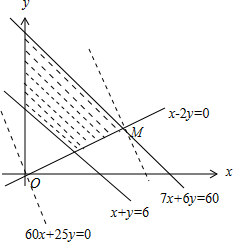
(Ⅱ)解:設總收視人次為z萬,則目標函數為z=60x+25y.
考慮z=60x+25y,將它變形為$y=-\frac{12}{5}x+\frac{z}{25}$,這是斜率為$-\frac{12}{5}$,隨z變化的一族平行直線.
$\frac{z}{25}$為直線在y軸上的截距,當$\frac{z}{25}$取得最大值時,z的值最大.
又∵x,y滿足約束條件,
∴由圖可知,當直線z=60x+25y經過可行域上的點M時,截距$\frac{z}{25}$最大,即z最大.
解方程組$\left\{\begin{array}{l}7x+6y=60\\ x-2y=0\end{array}\right.$,得點M的坐標為(6,3).
∴電視臺每周播出甲連續劇6次、乙連續劇3次時才能使總收視人次最多.
點評 本題考查解得線性規劃的應用,考查數學建模思想方法及數形結合的解題思想方法,是中檔題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
| A. | x=$\frac{2}{3}$π | B. | x=-$\frac{1}{12}$π | C. | x=$\frac{1}{3}$π | D. | x=$\frac{5}{12}$π |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {2} | B. | {1,2,4} | C. | {1,2,4,5} | D. | {x∈R|-1≤x≤5} |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{x^2}{4}-\frac{y^2}{12}=1$ | B. | $\frac{x^2}{12}-\frac{y^2}{4}=1$ | C. | $\frac{x^2}{3}-{y^2}=1$ | D. | ${x^2}-\frac{y^2}{3}=1$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [1,2] | B. | [2,4] | C. | [$\sqrt{7}$-1,$\sqrt{7}$+1] | D. | [$\sqrt{5}$-1,$\sqrt{5}$+1] |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | $\sqrt{3}$+1 | D. | $\sqrt{3}$+2 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
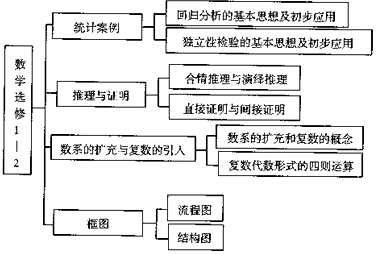
| A. | 推理與證明 | B. | 統計案例 | ||
| C. | 數系的擴充與復數的引入 | D. | 框圖 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
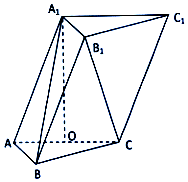 如圖,在三棱柱ABC-A1B1C1中,$AB=BC=\sqrt{5},AC=2$且點A1在底面ABC上的射影O恰是線段AC的中點,$A{A_1}=\sqrt{5}$.
如圖,在三棱柱ABC-A1B1C1中,$AB=BC=\sqrt{5},AC=2$且點A1在底面ABC上的射影O恰是線段AC的中點,$A{A_1}=\sqrt{5}$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com