
【題目】已知函數 ![]() 有最大值
有最大值 ![]() ,
, ![]() ,且
,且 ![]() 是
是 ![]() 的導數.
的導數.
(Ⅰ)求 ![]() 的值;
的值;
(Ⅱ)證明:當 ![]() ,
, ![]() 時,
時, ![]() .
.
【答案】解:(Ⅰ) ![]() 的定義域為
的定義域為 ![]() ,
, ![]() .
.
當 ![]() 時,
時, ![]() ,
,![]() 在
在 ![]() 上為單調遞增函數,無最大值,不合題意,舍去;
上為單調遞增函數,無最大值,不合題意,舍去;
當 ![]() 時,令
時,令 ![]() ,得
,得 ![]() ,
,
當 ![]() 時,
時, ![]() ,函數
,函數 ![]() 單調遞增;
單調遞增;
當 ![]() 時,
時, ![]() ,函數
,函數 ![]() 單調遞減,
單調遞減,![]() ,
,![]() ,
,![]() .
.
(Ⅱ)由(Ⅰ)可知, ![]() ,
,![]() .
.![]() ,
, ![]() ,
,![]() 在
在 ![]() 上單調遞增.
上單調遞增.
又 ![]() ,
, ![]() 且
且 ![]() ,
,![]() .
.![]() ,
,![]() 當
當 ![]() 時,
時, ![]() ,
, ![]() 單調遞增,
單調遞增,
要證 ![]() ,即
,即 ![]() ,只要證
,只要證 ![]() ,即
,即 ![]() .
.![]() ,
, ![]() ,
,
所以只要證 ![]()
![]()
![]() ————(*),
————(*),
設 ![]()
![]() (其中
(其中 ![]() ),
),![]() ,
,![]() 在(0,1)上為增函數,
在(0,1)上為增函數,![]() ,故(*)式成立,從而
,故(*)式成立,從而 ![]()
【解析】(Ⅰ)根據題目中所給的條件的特點,求出函數的導數,通過討論a的范圍,利用導數和函數的單調性的關系求出函數的單調區間;
(Ⅱ)求出函數的導數,根據函數的單調性問題進行等價轉化為函數的最值問題求解即可.主要考查導數的幾何意義、導數及其應用、不等式等基礎知識.
【考點精析】利用利用導數研究函數的單調性和函數的極值對題目進行判斷即可得到答案,需要熟知一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減;極值反映的是函數在某一點附近的大小情況.
在這個區間單調遞減;極值反映的是函數在某一點附近的大小情況.


科目:高中數學 來源: 題型:
【題目】若ax2+bx+c<0的解集為{x|x<-2,或x>4},則對于函數f(x)=ax2+bx+c應有( )
A.f(5)<f(2)<f(-1)
B.f(5)<f(-1)<f(2)
C.f(-1)<f(2)<f(5)
D.f(2)<f(-1)<f(5)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=-x2-2x,g(x)= 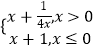
(1)求g[f(1)]的值;
(2)若方程g[f(x)]-a=0有4個實數根,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題中,真命題的個數為①對任意的a,b∈R,a>b是a|a|>b|b|的充要條件;②在△ABC中,若A>B,則sinA>sinB;③非零向量 ![]() ,若
,若 ![]() ,則向量
,則向量 ![]() 與向量
與向量 ![]() 的夾角為銳角;④
的夾角為銳角;④ ![]() .( )
.( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=lnx,g(x)= ![]() ﹣
﹣ ![]() (x為實常數).
(x為實常數).
(1)當a=1時,求函數φ(x)=f(x)﹣g(x)在x∈[4,+∞)上的最小值;
(2)若方程e2f(x)=g(x)(其中e=2.71828…)在區間[ ![]() ]上有解,求實數a的取值范圍.
]上有解,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com