
| A. | 2 | B. | $\frac{\sqrt{5}}{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
分析 根據|PQ|=2|QF1|,以及圓的性質,結合直角三角形的性質,建立三角形的邊角關系,利用雙曲線的定義得到關于a,c的方程進行求解即可.
解答 解:∵點P是以F1F2為直徑的圓與C右支的一個交點,
∴即∠F1PF2為直角,
∴則設|QF1|=m,|PQ|=2m,
則|F1F2|=2c,
則|PF2|=$\sqrt{4{c}^{2}-9{m}^{2}}$,|QF2|=$\sqrt{4{c}^{2}-5{m}^{2}}$,
則|PF1|-|PF2|=3m-$\sqrt{4{c}^{2}-9{m}^{2}}$=2a,①
|QF2|-|QF1|=$\sqrt{4{c}^{2}-5{m}^{2}}$-m=2a,②,
則3m-$\sqrt{4{c}^{2}-9{m}^{2}}$=$\sqrt{4{c}^{2}-5{m}^{2}}$-m=2a,
即4m-$\sqrt{4{c}^{2}-9{m}^{2}}$=$\sqrt{4{c}^{2}-5{m}^{2}}$,
平方整理得45m2=16c2,
則m2=$\frac{16}{45}$c2,代回②得$\sqrt{4{c}^{2}-5×\frac{16{c}^{2}}{45}}$-$\frac{4\sqrt{5}}{15}$c=2a,
即c=$\sqrt{5}$a
雙曲線的離心率e=$\frac{c}{a}$=$\sqrt{5}$,
故選D.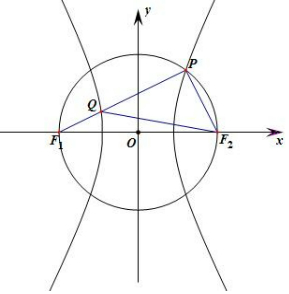
點評 本題主要考查雙曲線離心率的計算,根據直角三角形的邊角關系建立方程組,求出a,c的關系是解決本題的關鍵.綜合性較強,運算量較大,屬于中檔題.


科目:高中數學 來源: 題型:解答題
| 組別 | 步數分組 | 頻數 |
| A | 5500≤x<6500 | 2 |
| B | 6500≤x<7500 | 10 |
| C | 7500≤x<8500 | m |
| D | 8500≤x<9500 | 2 |
| E | 9500≤x<10500 | n |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | n>m>p | B. | p>m>n | C. | m>n>p | D. | m>p>n |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-$\frac{9}{4}$,-2]∪(0,$\frac{1}{2}$] | B. | (-$\frac{11}{4}$,-2]∪(0,$\frac{1}{2}$] | C. | (-$\frac{9}{4}$,-2]∪(0,$\frac{2}{3}$] | D. | (-$\frac{11}{4}$,-2]∪(0,$\frac{2}{3}$] |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
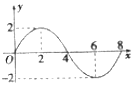 已知函數f(x)=Asin(ωx+ϕ)(A>0,ω>0,x≥0)的部分圖象如圖所示,則f(1)+f(2)+f(3)+…+f(11)的值等于( )
已知函數f(x)=Asin(ωx+ϕ)(A>0,ω>0,x≥0)的部分圖象如圖所示,則f(1)+f(2)+f(3)+…+f(11)的值等于( )| A. | 2 | B. | $2+\sqrt{2}$ | C. | $2+2\sqrt{2}$ | D. | $-2-\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{9}{28}$ | B. | $\frac{3}{8}$ | C. | $\frac{3}{7}$ | D. | $\frac{2}{7}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com