
分析 (1)根據(jù)向量坐標公式先求出向量坐標,根據(jù)向量數(shù)量積的坐標公式進行求解即可.
(2)根據(jù)向量數(shù)量積的應(yīng)用求出向量長度,進行求解即可.
解答 解:(1)∵$\overrightarrow a=({1,3}),\overrightarrow b=({m,2}),\overrightarrow c=({3,4})$,
∴$\overrightarrow{a}$-3$\overrightarrow{b}$=(1.3)-(3m,6)=(1-3m,-3),
∵$({\overrightarrow a-3\overrightarrow b})⊥\overrightarrow c$,
∴($\overrightarrow{a}$-3$\overrightarrow{b}$)•$\overrightarrow{c}$=3(1-3m)+(-3)×4=-9m-9=0,
得m=-1.
(2)由(1)知,$\overrightarrow{a}$=(1,3),$\overrightarrow{b}$=(-1,2),
則$\overrightarrow{a}$•$\overrightarrow{b}$=5,|$\overrightarrow{a}$|=$\sqrt{10}$,|$\overrightarrow{b}$|=$\sqrt{5}$,
則cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=$\frac{5}{\sqrt{10}×\sqrt{5}}$=$\frac{\sqrt{2}}{2}$,
∵θ∈(0,π),
∴θ=$\frac{π}{4}$.
點評 本題主要考查向量數(shù)量積的應(yīng)用,根據(jù)向量垂直與向量數(shù)量積的關(guān)系以及向量夾角與向量數(shù)量積的關(guān)系是解決本題的關(guān)鍵.


 同步練習(xí)河南大學(xué)出版社系列答案
同步練習(xí)河南大學(xué)出版社系列答案 同步練習(xí)西南師范大學(xué)出版社系列答案
同步練習(xí)西南師范大學(xué)出版社系列答案科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 0.2 | B. | 0.6 | C. | 0.4 | D. | 0.3 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
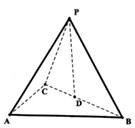 如圖,三棱錐P-ABC中,D是BC的中點,△PAB為等邊三角形,△ABC為等腰直角三角形,AB=AC=4,且二面角P-AB-D的余弦值為$\frac{\sqrt{3}}{3}$.
如圖,三棱錐P-ABC中,D是BC的中點,△PAB為等邊三角形,△ABC為等腰直角三角形,AB=AC=4,且二面角P-AB-D的余弦值為$\frac{\sqrt{3}}{3}$.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | $[\frac{2}{3},1)$ | B. | $[\frac{1}{3},1)$ | C. | $[\frac{1}{3},1)∪(1,3]$ | D. | (1,3] |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | -2 | B. | 2 | C. | -1 | D. | 1 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | ±1 | B. | ±2 | C. | $±\sqrt{2}$ | D. | $±\sqrt{3}$ |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com