
【題目】如圖![]() ,在邊長為
,在邊長為![]() 的菱形
的菱形![]() 中,
中,![]() ,現沿對角線
,現沿對角線![]() 把
把![]() 翻折到
翻折到![]() 的位置得到四面體
的位置得到四面體![]() ,如圖
,如圖![]() 所示.已知
所示.已知![]() .
.

(1)求證:平面![]() 平面
平面![]() ;
;
(2)若![]() 是線段
是線段![]() 上的點,且
上的點,且![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)證明見解析;(2)![]() .
.
【解析】
(1)取![]() 的中點
的中點![]() ,連接
,連接![]() 、
、![]() ,推導出
,推導出![]() 、
、![]() ,利用線面垂直的判定定理得出
,利用線面垂直的判定定理得出![]() 平面
平面![]() ,再利用面面垂直的判定定理可證得平面
,再利用面面垂直的判定定理可證得平面![]() 平面
平面![]() ;
;
(2)推導出![]() 、
、![]() 、
、![]() 兩兩垂直,以
兩兩垂直,以![]() 為坐標原點,
為坐標原點,![]() 、
、![]() 、
、![]() 所在直線分別為
所在直線分別為![]() 軸、
軸、![]() 軸、
軸、![]() 軸建立空間直角坐標系
軸建立空間直角坐標系![]() ,計算出向量
,計算出向量![]() 的坐標,利用空間向量法可求得二面角
的坐標,利用空間向量法可求得二面角![]() 的余弦值.
的余弦值.
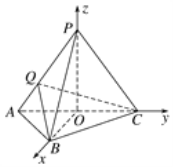
(1)在三棱錐![]() 中,取
中,取![]() 的中點
的中點![]() ,連接
,連接![]() 、
、![]() ,得到
,得到![]() ,
,
![]() 四邊形
四邊形![]() 是菱形,
是菱形,![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,![]() 、
、![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() ;
;
(2)![]() ,
,![]() 為
為![]() 中點,
中點,![]() ,
,![]() 、
、![]() 、
、![]() 兩兩垂直,
兩兩垂直,
以![]() 為坐標原點,
為坐標原點,![]() 、
、![]() 、
、![]() 所在直線分別為
所在直線分別為![]() 軸、
軸、![]() 軸、
軸、![]() 軸建立如圖所示的空間直角坐標系
軸建立如圖所示的空間直角坐標系![]() ,
,
則![]() 、
、![]() 、
、![]() 、
、![]() ,
,
![]() ,
,![]() ,
,
設平面![]() 的法向量
的法向量![]() ,
,
由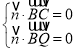 ,即
,即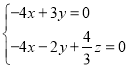 ,解得
,解得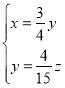 ,取
,取![]() ,則
,則![]() ,
,
易知平面![]() 的一個法向量為
的一個法向量為![]() ,
,
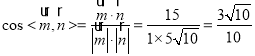 .
.
由圖可知二面角![]() 為銳角,所以,二面角
為銳角,所以,二面角![]() 的余弦值為
的余弦值為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】如圖,四邊形ABCD是正方形,G是線段AD延長線一點,![]() ,
,![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,F是線段PG的中點;
,F是線段PG的中點;

![]() 求證:
求證:![]() 平面PAC;
平面PAC;
![]() 若
若![]() 時,求平面PCF與平面PAG所成二面角的余弦值.
時,求平面PCF與平面PAG所成二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】1642年,帕斯卡發明了一種可以進行十進制加減法的機械計算機![]() 年,萊布尼茨改進了帕斯卡的計算機,但萊布尼茲認為十進制的運算在計算機上實現起來過于復雜,隨即提出了“二進制”數的概念
年,萊布尼茨改進了帕斯卡的計算機,但萊布尼茲認為十進制的運算在計算機上實現起來過于復雜,隨即提出了“二進制”數的概念![]() 之后,人們對進位制的效率問題進行了深入的研究
之后,人們對進位制的效率問題進行了深入的研究![]() 研究方法如下:對于正整數
研究方法如下:對于正整數![]() ,
,![]() ,我們準備
,我們準備![]() 張不同的卡片,其中寫有數字0,1,…,
張不同的卡片,其中寫有數字0,1,…,![]() 的卡片各有
的卡片各有![]() 張
張![]() 如果用這些卡片表示
如果用這些卡片表示![]() 位
位![]() 進制數,通過不同的卡片組合,這些卡片可以表示
進制數,通過不同的卡片組合,這些卡片可以表示![]() 個不同的整數
個不同的整數![]() 例如
例如![]() ,
,![]() 時,我們可以表示出
時,我們可以表示出![]() 共
共![]() 個不同的整數
個不同的整數![]() 假設卡片的總數
假設卡片的總數![]() 為一個定值,那么
為一個定值,那么![]() 進制的效率最高則意味著
進制的效率最高則意味著![]() 張卡片所表示的不同整數的個數
張卡片所表示的不同整數的個數![]() 最大
最大![]() 根據上述研究方法,幾進制的效率最高?
根據上述研究方法,幾進制的效率最高?![]()
![]()
A. 二進制 B. 三進制 C. 十進制 D. 十六進制
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的最大值為
的最大值為![]() ,其圖像相鄰的兩條對稱軸之間的距離為
,其圖像相鄰的兩條對稱軸之間的距離為![]() ,且
,且![]() 的圖像關于點
的圖像關于點![]() 對稱,則下列結論正確的是( ).
對稱,則下列結論正確的是( ).
A.函數![]() 的圖像關于直線
的圖像關于直線![]() 對稱
對稱
B.當![]() 時,函數
時,函數![]() 的最小值為
的最小值為![]()
C.若![]() ,則
,則![]() 的值為
的值為![]()
D.要得到函數![]() 的圖像,只需要將
的圖像,只需要將![]() 的圖像向右平移
的圖像向右平移![]() 個單位
個單位
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】田忌賽馬是![]() 史記
史記![]() 中記載的一個故事,說的是齊國將軍田忌經常與齊國眾公子賽馬,孫臏發也們的馬腳力都差不多,都分為上、中、下三等
中記載的一個故事,說的是齊國將軍田忌經常與齊國眾公子賽馬,孫臏發也們的馬腳力都差不多,都分為上、中、下三等![]() 于是孫臏給田忌將軍制定了一個必勝策略:比賽即將開始時,他讓田忌用下等馬對戰公子們的上等馬,用上等馬對戰公子們的中等馬,用中等馬對戰公子們的下等馬,從而使田忌贏得公子們許多賭注
于是孫臏給田忌將軍制定了一個必勝策略:比賽即將開始時,他讓田忌用下等馬對戰公子們的上等馬,用上等馬對戰公子們的中等馬,用中等馬對戰公子們的下等馬,從而使田忌贏得公子們許多賭注![]() 假設田忌的各等級馬與某公子的各等級馬進行一場比賽獲勝的概率如表所示:
假設田忌的各等級馬與某公子的各等級馬進行一場比賽獲勝的概率如表所示:
田忌的馬 | 上等馬 | 中等馬 | 下等馬 |
上等馬 |
|
| 1 |
中等馬 |
|
|
|
下等馬 | 0 |
|
|
比賽規則規定:一次比由三場賽馬組成,每場由公子和田忌各出一匹馬出騫,結果只有勝和負兩種,并且毎一方三場賽馬的馬的等級各不相同,三場比賽中至少獲勝兩場的一方為最終勝利者.
![]() 如果按孫臏的策略比賽一次,求田忌獲勝的概率;
如果按孫臏的策略比賽一次,求田忌獲勝的概率;
![]() 如果比賽約定,只能同等級馬對戰,每次比賽賭注1000金,即勝利者贏得對方1000金,每月比賽一次,求田忌一年賽馬獲利的數學期望.
如果比賽約定,只能同等級馬對戰,每次比賽賭注1000金,即勝利者贏得對方1000金,每月比賽一次,求田忌一年賽馬獲利的數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲乙兩人各有三張卡片,甲的卡片分別標有數字1、2、3,乙的卡片分別標有數字0、1、3.兩人各自隨機抽出一張,甲抽出的卡片上的數字記為![]() ,乙抽出的卡片上的數字記為
,乙抽出的卡片上的數字記為![]() ,則
,則![]() 與
與![]() 的積為奇數的概率為________.
的積為奇數的概率為________.
查看答案和解析>>
科目:高中數學 來源: 題型:
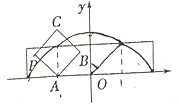
【題目】如圖放置的邊長為1的正方形![]() 沿
沿![]() 軸滾動,點
軸滾動,點![]() 恰好經過原點.設頂點
恰好經過原點.設頂點![]() 的軌跡方程是
的軌跡方程是![]() ,則對函數
,則對函數![]() 有下列判斷:①函數
有下列判斷:①函數![]() 是偶函數;②對任意的
是偶函數;②對任意的![]() ,都有
,都有![]() ;③函數
;③函數![]() 在區間
在區間![]() 上單調遞減;④函數
上單調遞減;④函數![]() 的值域是
的值域是![]() ;⑤
;⑤![]() .其中判斷正確的序號是__________.
.其中判斷正確的序號是__________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com