【題目】如圖，四邊形ABCD是正方形，G是線段AD延長線一點，
，
平面ABCD，
，
，F是線段PG的中點；
求證：
平面PAC；
若
時，求平面PCF與平面PAG所成二面角的余弦值．
【答案】（1）見解析；（2）
【解析】
分別連接DB，DF，可得四邊形BDFE為平行四邊形，
又
面PAC，即可得
平面PAC；
分別以直線AB，AG，AP為x軸，y軸，z軸建立空間直角坐標系，求得平面PCF的法向量
，平面PAG的法向量為
，即可得平面PCF與平面PAG所成二面角的余弦值．
證明：分別連接DB，DF，
，F分別是線段AG，PG的中點，
，
，
又
，
，
四邊形BDFE為平行四邊形．
．
四邊形ABCD時正方形，
，
平面ABCD，
，
，AC是面PAC內兩兩相交直線，
面PAC，
平面PAC；
解：分別以直線AB，AG，AP為x軸，y軸，z軸建立空間直角坐標系，
，
2，
，
2，
，
0，
，
，
．
設平面PCF的法向量，由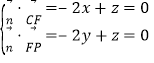
．
．
平面PAG的法向量為
．
平面PCF與平面PAG所成二面角的余弦值為．
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】高考改革后，學生除了語數外三門必選外，可在A類科目：物理、化學、生物和B類科目：政治、地理、歷史共6個科目中任選3門．
（1）若小明同學已經確定選了物理，現在他還要從剩余的5科中再選2科，則他在歷史與地理兩科中至少選一科的概率？
（2）求小明同學選A類科目數X的分布列、數學期望和方差．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知拋物線
的準線與雙曲線
相交于
、
兩點，雙曲線的一條漸近線方程是
，點
是拋物線的焦點，且
是等邊三角形，則該雙曲線的標準方程是( )
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖
，在邊長為
的菱形
中，
，現沿對角線
把
翻折到
的位置得到四面體
，如圖
所示.已知
.
（1）求證：平面
平面
；
（2）若
是線段
上的點，且
，求二面角
的余弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】將楊輝三角中的奇數換成1，偶數換成0，便可以得到如圖的“0-1三角”.在“
三角”中，從第1行起，設第n
次出現全行為1時，1的個數為
，則
等于（ ）
A.13B.14C.15D.16
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
