
【題目】在四棱錐P-ABCD中,側面![]() 底面ABCD,
底面ABCD,![]() ,底面ABCD是直角梯形,
,底面ABCD是直角梯形,![]()
![]()
![]()
![]() .
.

(1)求證:![]() 平面PBD:
平面PBD:
(2)設E為側棱PC上異于端點的一點,![]() ,試確定
,試確定![]() 的值,使得二面角E-BD-P的余弦值為
的值,使得二面角E-BD-P的余弦值為![]() .
.
 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】已知某地區中小學生人數和近視情況分別如圖1和圖2所示,為了解該地區中小學生的近視形成原因,用分層抽樣的方法抽取2%的學生進行調查,則樣本容量和抽取的高中生近視人數分別是( )
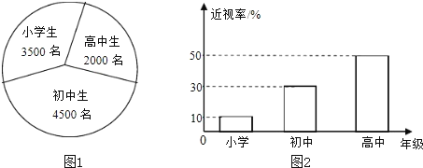
A.100,10B.100,20C.200,10D.200,20
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4—4:坐標系與參數方程]:在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (t為參數,
(t為參數,![]() ),以坐標原點為極點,以x軸的非負半軸為極軸,建立極坐標系,曲線C的極坐標方程為
),以坐標原點為極點,以x軸的非負半軸為極軸,建立極坐標系,曲線C的極坐標方程為![]() ,已知直線
,已知直線![]() 與曲線C交于不同的兩點A,B.
與曲線C交于不同的兩點A,B.
(1)求直線![]() 的普通方程和曲線C的直角坐標方程;
的普通方程和曲線C的直角坐標方程;
(2)設P(1,2),求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱柱ABCD-A1B1C1D1中,側棱AA1⊥底面ABCD,AB∥DC,![]()
![]()
![]() .
.

(Ⅰ)求證:CD⊥平面ADD1A1;
(Ⅱ)若直線AA1與平面AB1C所成角的正弦值為![]() ,求k的值.
,求k的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于給定的正整數k,若數列{an}滿足![]()
=2kan對任意正整數n(n> k) 總成立,則稱數列{an} 是“P(k)數列”.
(1)證明:等差數列{an}是“P(3)數列”;
若數列{an}既是“P(2)數列”,又是“P(3)數列”,證明:{an}是等差數列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() 為參數),以
為參數),以![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,點
,點![]() 是曲線
是曲線![]() 上的動點,點
上的動點,點![]() 在
在![]() 的延長線上,且
的延長線上,且![]() ,點
,點![]() 的軌跡為
的軌跡為![]() .
.
(1)求直線![]() 及曲線
及曲線![]() 的極坐標方程;
的極坐標方程;
(2)若射線![]() 與直線
與直線![]() 交于點
交于點![]() ,與曲線
,與曲線![]() 交于點
交于點![]() (與原點不重合),求
(與原點不重合),求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 的圓心為
的圓心為![]() ,且直線
,且直線![]() 與圓
與圓![]() 相切,設直線
相切,設直線![]() 的方程為
的方程為![]() ,若點
,若點![]() 在直線
在直線![]() 上,過點
上,過點![]() 作圓
作圓![]() 的切線
的切線![]() ,切點為
,切點為![]() .
.
(1)求圓![]() 的標準方程;
的標準方程;
(2)若![]() ,試求點
,試求點![]() 的坐標;
的坐標;
(3)若點![]() 的坐標為
的坐標為![]() ,過點
,過點![]() 作直線與圓
作直線與圓![]() 交于
交于![]() 兩點,當
兩點,當![]() 時,求直線
時,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
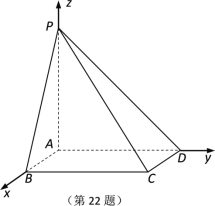
【題目】如圖所示,在四棱錐![]() 中,底面
中,底面![]() 是矩形,
是矩形,![]() 平面
平面![]() ,AB 1,AP AD 2.
,AB 1,AP AD 2.
(1)求直線![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;
(2)若點M,N分別在AB,PC上,且![]() 平面
平面![]() ,試確定點M,N的位置.
,試確定點M,N的位置.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com