
【題目】[選修4—4:坐標系與參數方程]:在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (t為參數,
(t為參數,![]() ),以坐標原點為極點,以x軸的非負半軸為極軸,建立極坐標系,曲線C的極坐標方程為
),以坐標原點為極點,以x軸的非負半軸為極軸,建立極坐標系,曲線C的極坐標方程為![]() ,已知直線
,已知直線![]() 與曲線C交于不同的兩點A,B.
與曲線C交于不同的兩點A,B.
(1)求直線![]() 的普通方程和曲線C的直角坐標方程;
的普通方程和曲線C的直角坐標方程;
(2)設P(1,2),求![]() 的取值范圍.
的取值范圍.
科目:高中數學 來源: 題型:
【題目】如圖,在正四棱錐S-ABCD中,E,M,N分別是BC,CD,SC的中點,動點P在線段MN上運動時,下列四個結論:①EP⊥AC;②EP∥BD;③EP∥平面SBD;④EP⊥平面SAC,其中恒成立的為( )
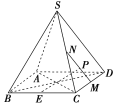
A.①③B.③④C.①②D.②③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】重慶近年來旅游業高速發展,有很多著名景點,如洪崖洞、磁器口、朝天門、李子壩等.為了解端午節當日朝天門景點游客年齡的分布情況,從年齡在22~52歲之間的旅游客中隨機抽取了1000人,制作了如圖的頻率分布直方圖.

(1)求抽取的1000人的年齡的平均數、中位數;(每一組的年齡取中間值)
(2)現從![]() 中按照分層抽樣抽取8人,再從這8人中隨機抽取3人,記這3人中年齡在
中按照分層抽樣抽取8人,再從這8人中隨機抽取3人,記這3人中年齡在![]() 的人數為
的人數為![]() ,求
,求![]() 的分布列及
的分布列及![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有一名高二學生盼望2020年進入某名牌大學學習,假設該名牌大學有以下條件之一均可錄取:①2020年2月通過考試進入國家數學奧賽集訓隊(集訓隊從2019年10月省數學競賽一等獎中選拔):②2020年3月自主招生考試通過并且達到2020年6月高考重點分數線,③2020年6月高考達到該校錄取分數線(該校錄取分數線高于重點線),該學生具備參加省數學競賽、自主招生和高考的資格且估計自己通過各種考試的概率如下表
省數學競賽一等獎 | 自主招生通過 | 高考達重點線 | 高考達該校分數線 |
0.5 | 0.6 | 0.9 | 0.7 |
若該學生數學競賽獲省一等獎,則該學生估計進入國家集訓隊的概率是0.2.若進入國家集訓隊,則提前錄取,若未被錄取,則再按②、③順序依次錄取:前面已經被錄取后,不得參加后面的考試或錄取.(注:自主招生考試通過且高考達重點線才能錄取)
(Ⅰ)求該學生參加自主招生考試的概率;
(Ⅱ)求該學生參加考試的次數![]() 的分布列及數學期望;
的分布列及數學期望;
(Ⅲ)求該學生被該校錄取的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() .
.
(1)若直線不經過第四象限,求![]() 的取值范圍;
的取值范圍;
(2)若直線![]() 交
交![]() 軸負半軸于
軸負半軸于![]() ,交
,交![]() 軸正半軸于
軸正半軸于![]() ,求
,求![]() 的面積的最小值并求此時直線
的面積的最小值并求此時直線![]() 的方程;
的方程;
(3)已知點![]() ,若點
,若點![]() 到直線
到直線![]() 的距離為
的距離為![]() ,求
,求![]() 的最大值并求此時直線
的最大值并求此時直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面ABCD為梯形,AB//CD,
中,底面ABCD為梯形,AB//CD,![]() ,AB=AD=2CD=2,△ADP為等邊三角形.
,AB=AD=2CD=2,△ADP為等邊三角形.

(1)當PB長為多少時,平面![]() 平面ABCD?并說明理由;
平面ABCD?并說明理由;
(2)若二面角![]() 大小為150°,求直線AB與平面PBC所成角的正弦值.
大小為150°,求直線AB與平面PBC所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,正方體ABCD-A1B1C1D1的棱長為1,線段B1D1上有兩個動點E、F且EF=![]() ,則下列結論中錯誤的是( )
,則下列結論中錯誤的是( )

A.AC⊥BEB.EF![]() 平面ABCD
平面ABCD
C.三棱錐A-BEF的體積為定值D.異面直線AE,BF所成的角為定值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在四棱錐P-ABCD中,側面![]() 底面ABCD,
底面ABCD,![]() ,底面ABCD是直角梯形,
,底面ABCD是直角梯形,![]()
![]()
![]()
![]() .
.

(1)求證:![]() 平面PBD:
平面PBD:
(2)設E為側棱PC上異于端點的一點,![]() ,試確定
,試確定![]() 的值,使得二面角E-BD-P的余弦值為
的值,使得二面角E-BD-P的余弦值為![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)當![]() 時,證明函數
時,證明函數![]() 是增函數;
是增函數;
(2)是否存在實數![]() ,使得只有唯一的正數
,使得只有唯一的正數![]() ,當
,當![]() 時恒有:
時恒有:![]() ,若這樣的實數
,若這樣的實數![]() 存在,試求
存在,試求![]() 、
、![]() 的值,若不存在,請說明理由.
的值,若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com