
 ln(2x+1)萬美元,受美聯儲貨幣政策的影響,美元?值,由于生產加工簽約和成品交付要經歷一段時間,收益將因美元賠值而損失mx萬美元,其中m為該時段美元的貶值指數是m∈(0,1),從而實際所得的加工費為f(x)=
ln(2x+1)萬美元,受美聯儲貨幣政策的影響,美元?值,由于生產加工簽約和成品交付要經歷一段時間,收益將因美元賠值而損失mx萬美元,其中m為該時段美元的貶值指數是m∈(0,1),從而實際所得的加工費為f(x)= ln(2x+1)-mx(萬美元).
ln(2x+1)-mx(萬美元).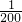 ,為確保企業實際所得加工費隨X的增加而增加,該企業加工產品訂單的金額X應在什么范圍內?
,為確保企業實際所得加工費隨X的增加而增加,該企業加工產品訂單的金額X應在什么范圍內? x萬美元,己知該企業加工生產能力為x∈[10,20](其中X為產品訂單的金額),試問美元的貶值指數m在何范圍時,該企業加工生產將不會出現虧損.
x萬美元,己知該企業加工生產能力為x∈[10,20](其中X為產品訂單的金額),試問美元的貶值指數m在何范圍時,該企業加工生產將不會出現虧損.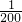 ,f(x)=
,f(x)= ln(2x+1)-
ln(2x+1)-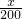 ,(其中x>0);
,(其中x>0);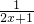 -
-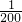 =
= ;
; ln(2x+1)-mx≥
ln(2x+1)-mx≥ x,即
x,即 +m≤
+m≤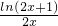 ,
,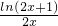 ,x∈[10,20],則
,x∈[10,20],則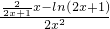 =
=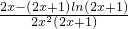 ;
;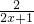 ]=-2ln(2x+1)<0,
]=-2ln(2x+1)<0,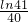 ,即m≤
,即m≤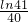 -
- ;
;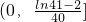 時,該企業加工生產不會虧損.
時,該企業加工生產不會虧損.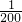 ,得f(x)=
,得f(x)= ln(2x+1)-
ln(2x+1)-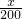 ,對f(x)求導,并令f′(x)>0,可解得x的值;即為所求.
,對f(x)求導,并令f′(x)>0,可解得x的值;即為所求. ln(2x+1)-mx≥
ln(2x+1)-mx≥ x恒成立,通過變形,得
x恒成立,通過變形,得 +m≤
+m≤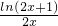 ,令g(x)=
,令g(x)=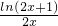 ,x∈[10,20],對g(x)求導,得g′(x)=
,x∈[10,20],對g(x)求導,得g′(x)=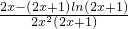 ;再令h(x)=2x-(2x+1)ln(2x+1),對h(x)求導,得h′(x)<0,從而得h(x)在[10,20]上單調遞減,即h(20)≤h(x)≤h(10)<0,所以x∈[10,20]時,g(x)單調遞減,從而得gmin(x)=g(20),即m≤g(20)-
;再令h(x)=2x-(2x+1)ln(2x+1),對h(x)求導,得h′(x)<0,從而得h(x)在[10,20]上單調遞減,即h(20)≤h(x)≤h(10)<0,所以x∈[10,20]時,g(x)單調遞減,從而得gmin(x)=g(20),即m≤g(20)- ;即得美元的貶值指數m的范圍.
;即得美元的貶值指數m的范圍.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:單選題
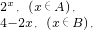 x0∈A,且f[f(x0)]∈A,則x0的取值范圍是
x0∈A,且f[f(x0)]∈A,則x0的取值范圍是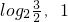 )
)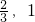 )
) ]
]查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 高校 | 相關人數 | 抽取人數 |
| A | X | 1 |
| B | 36 | y |
| C | 54 | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
 的雙曲線C2以A,B為焦點.若P是圓C1與雙曲線C2的一個公共點,則|PA|+|PB|=
的雙曲線C2以A,B為焦點.若P是圓C1與雙曲線C2的一個公共點,則|PA|+|PB|=



查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
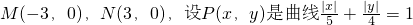 上的點,則下列式子恒成立的是
上的點,則下列式子恒成立的是查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com