
自駕游從A地到B地有甲乙兩條線路,甲線路是A-C-D-B,乙線路是A-E-F-G-H-B,其中CD段,EF段,GH段都是易堵車路段.假設這三條路段堵車與否相互獨立.這三條路段的堵車概率及平均堵車時間如表所示.
| CD段 | EF段 | GH段 |
堵車概率 |
|
|
|
平均堵車時間 (單位:小時) |
| 2 | 1 |
經調查發現,堵車概率 在
在 上變化,
上變化, 在
在 上變化.
上變化.
在不堵車的情況下,走甲線路需汽油費500元,走乙線路需汽油費545元.而每堵車1小時,需多花汽油費20元.路政局為了估計 段平均堵車時間,調查了100名走甲線路的司機,得到下表數據.
段平均堵車時間,調查了100名走甲線路的司機,得到下表數據.
堵車時間(單位:小時) | 頻數 |
[0,1] | 8 |
(1, 2] | 6 |
(2, 3] | 38 |
(3, 4] | 24 |
(4, 5] | 24 |
(1)求 段平均堵車時間
段平均堵車時間 的值;
的值;
(2)若只考慮所花汽油費的期望值大小,為了節約,求選擇走甲線路的概率.
(1)3;(2)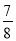 .
.
【解析】
試題分析:本題考查利用頻率分布表求平均數,相互獨立事件同時發生的概率,離散型隨機變量分布列,數學期望,幾何概型等基礎知識;考查運用統計、概率、數學期望等數學知識解決實際問題的能力,以及運算求解能力;考查數形結合數學思想方法.第一問,用總的堵車時間除以總人數100人,即得到平均堵車時間;第二問,利用獨立事件求出每種情況的概率,選擇甲路線說明甲需汽油費少,利用線性規劃化畫出區域圖,再利用幾何概型求概率;法二,分別求EF路段和GH路段的期望再相加求乙路線多花汽油費的期望.
試題解析:(1)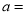
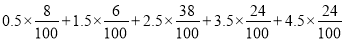 2分
2分
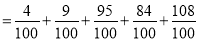
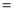 3. 4分
3. 4分
(2)設走甲線路所花汽油費為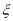 元,
元,
則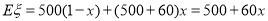 . 5分
. 5分
法一:設走乙線路多花的汽油費為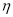 元,∵
元,∵ 段與
段與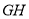 段堵車與否相互獨立,
段堵車與否相互獨立,
∴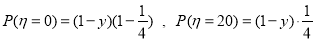 ,
,
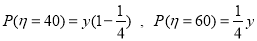 , 7分
, 7分
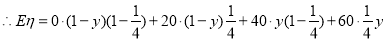
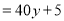 . 8分
. 8分
∴走乙線路所花的汽油費的數學期望為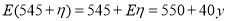 . 9分
. 9分
依題意,選擇走甲線路應滿足 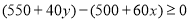 , 10分
, 10分
即 ,又
,又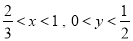 ,
,
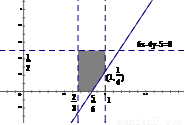
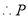 (選擇走甲線路)
(選擇走甲線路) . 13分
. 13分
法二:在EF路段多花汽油費的數學期望是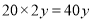 元, 6分
元, 6分
在GH路段多花汽油費的數學期望是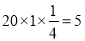 元, 7分
元, 7分
因為EF、GH路段堵車與否相互獨立,
所以走乙路線多花汽油費的數學期望是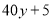 元. 8分
元. 8分
以下解法同法一.
考點:利用頻率分布表求平均數,相互獨立事件同時發生的概率,離散型隨機變量分布列,數學期望,幾何概型.


科目:高中數學 來源:2013-2014學年福建省福州市高三5月綜合練習文科數學試卷(解析版) 題型:選擇題
某公司的一品牌電子產品,2013年年初,由于市場疲軟,產品銷售量逐漸下降,五月份公司加大了宣傳力度,銷售量出現明顯的回升,九月份,公司借大學生開學之際,采取了促銷等手段,產品的銷售量猛增,十一月份之后,銷售量有所回落.下面大致能反映出公司2013年該產品銷售量的變化情況的圖象是( )

查看答案和解析>>
科目:高中數學 來源:2013-2014學年福建省高考考前模擬文科數學試卷(解析版) 題型:選擇題
已知曲線 :
: 和
和 :
: 的焦點分別為
的焦點分別為 、
、 ,點
,點 是
是 和
和 的一個交點,則△
的一個交點,則△ 的形狀是( )
的形狀是( )
A.銳角三角形 B.直角三角形 C.鈍角三角形 D.都有可能
查看答案和解析>>
科目:高中數學 來源:2013-2014學年福建省漳州市畢業班質量檢查理科數學試卷(解析版) 題型:選擇題
已知正三角形ABC的頂點A(1,1),B(1,3),頂點C在第一象限,若點(x,y)在△ABC內部,則z=-x+y的取值范圍是
A.(1-,2) B.(0,2) C.(-1,2) D.(0,1+)
查看答案和解析>>
科目:高中數學 來源:2013-2014學年福建省漳州市畢業班質量檢查理科數學試卷(解析版) 題型:選擇題
已知1是虛數單位,則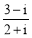 等于
等于
A.-1+1 B.-1-1 C.1+1 D.1-1
查看答案和解析>>
科目:高中數學 來源:2013-2014學年福建省廈門市高三5月適應性考試理科數學試卷(解析版) 題型:選擇題
數列 的前
的前 項和為
項和為 ,前
,前 項積為
項積為 ,且
,且 ,則
,則 等于( )
等于( )
 A.31 B.62 C.124 D.126
A.31 B.62 C.124 D.126
查看答案和解析>>
科目:高中數學 來源:2013-2014學年福建省三明市高三5月質量檢查文科數學試卷(解析版) 題型:選擇題
對于函數 在定義域內的任意實數
在定義域內的任意實數 及
及 ,都有
,都有 及
及
 成立,則稱函數
成立,則稱函數 為“
為“ 函數”.現給出下列四個函數:
函數”.現給出下列四個函數:


 ;
; .其中是“
.其中是“ 函數”的是( )
函數”的是( )
A. B.
B. C.
C.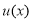 D.
D.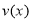
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com