
分析 聯立y=sinx與y=cosx求出在[0,$\frac{π}{2}$]內的交點P坐標,然后求出該點處兩切線方程,從而求出三角形的三個頂點坐標,最后根據三角形面積公式求解.
解答 解:由sinx=cosx,且x∈[0,$\frac{π}{2}$],得x=$\frac{π}{4}$,
∴y=sinx與y=cosx在[0,$\frac{π}{2}$]內的交點P的坐標是($\frac{π}{4}$,$\frac{\sqrt{2}}{2}$),
函數y=sinx與y=cosx的導函數分別為y=cosx與y=-sinx,
則兩函數在($\frac{π}{4}$,$\frac{\sqrt{2}}{2}$)處的切線的斜率分別為$\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2}$.
得兩條切線方程分別是y-$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}}{2}$(x-$\frac{π}{4}$)和y-$\frac{\sqrt{2}}{2}$=-$\frac{\sqrt{2}}{2}$(x-$\frac{π}{4}$),
y=0時,x=$\frac{π}{4}$-1,x=$\frac{π}{4}$+1,
于是三角形三頂點坐標分別為($\frac{π}{4}$,$\frac{\sqrt{2}}{2}$),($\frac{π}{4}$-1,0),($\frac{π}{4}$+1,0),
S=$\frac{1}{2}$×2×$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}}{2}$,
即它們與x軸所圍成的三角形的面積是$\frac{\sqrt{2}}{2}$,
故答案為:$\frac{\sqrt{2}}{2}$.
點評 本題主要考查了利用導數研究函數的再某點切線方程,以及三角方程和三角形面積公式,屬于中檔題.


科目:高中數學 來源: 題型:填空題
| x | 197 | 198 | 201 | 204 | 205 |
| y | 1 | 3 | 6 | 7 | m |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| x | 3.5 | 4.5 | 5.5 | 6.5 |
| y | 3 | 4m | 4 | 5 |
| A. | 1 | B. | 0.85 | C. | 0.95 | D. | 0.9 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
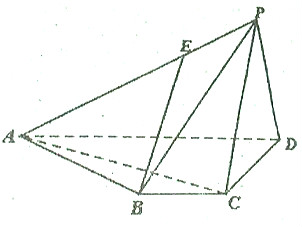 如圖,四棱錐P-ABCD中,BC∥AD,BC=1,AD=3,AC⊥CD,且平面PCD⊥平面ABCD.
如圖,四棱錐P-ABCD中,BC∥AD,BC=1,AD=3,AC⊥CD,且平面PCD⊥平面ABCD.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -2 | B. | 2 | C. | -1 | D. | 1 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com