
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{10}$ | D. | $\frac{2}{5}$ |
分析 先求出基本事件總數n=5×5=25,再用列舉法求出抽得的第一張卡片上的數大于第二張卡片上的數包含的基本事件個數,由此能求出抽得的第一張卡片上的數大于第二張卡片上的數的概率.
解答 解:從分別寫有1,2,3,4,5的5張卡片中隨機抽取1張,放回后再隨機抽取1張,
基本事件總數n=5×5=25,
抽得的第一張卡片上的數大于第二張卡片上的數包含的基本事件有:
(2,1),(3,1),(3,2),(4,1),(4,2),(4,3),(5,1),(5,2),(5,3),(5,4),
共有m=10個基本事件,
∴抽得的第一張卡片上的數大于第二張卡片上的數的概率p=$\frac{10}{25}$=$\frac{2}{5}$.
故選:D.
點評 本題考查概率的求法,是基礎題,解題時要認真審題,注意列舉法的合理運用.


 開心快樂假期作業暑假作業西安出版社系列答案
開心快樂假期作業暑假作業西安出版社系列答案 名題訓練系列答案
名題訓練系列答案 期末集結號系列答案
期末集結號系列答案科目:高中數學 來源: 題型:選擇題
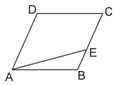 已知菱形ABCD中,∠A=$\frac{π}{3}$,AB=1,E為BC邊上任一點,則$\overrightarrow{AE}$•$\overrightarrow{EC}$的最大值為( )
已知菱形ABCD中,∠A=$\frac{π}{3}$,AB=1,E為BC邊上任一點,則$\overrightarrow{AE}$•$\overrightarrow{EC}$的最大值為( )| A. | $\frac{1}{3}$ | B. | $\frac{9}{16}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-2,2) | B. | (-∞,-2)∪(2,+∞) | C. | [-2,2] | D. | (-∞,-2]∪[2,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 是奇函數,且在R上是增函數 | B. | 是偶函數,且在R上是增函數 | ||
| C. | 是奇函數,且在R上是減函數 | D. | 是偶函數,且在R上是減函數 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com