
分析 (1)當a=2時,利用導數即可判斷函數f(x)的單調性.
(2)a=4,先求導,再根據基本不等式得到f′(x)≥4$\sqrt{2}$-6,不存在6x+y+m=0這類直線的切線,存在3x-y+n=0這類直線的切線
(3)問題等價于y=g(x)=$\frac{{2x}_{0}^{2}-6{x}_{0}+4}{{x}_{0}}$(x-x0)+x02-6x0+4lnx0,令$ϕ(x)={x_0}{x^2}-(2{x^2}_0+4)x+4lnx•{x_0}+x_0^3+4{x_0}-4ln{x_0}•{x_0}$,由此入手,能夠求出一個“類對稱點”的橫坐標.
解答 解:(1)函數f(x)的定義域是(0,+∞).
∵f(x)=x2-4x+2lnx,
∴$f'(x)=2x-4+\frac{2}{x}=\frac{{2{x^2}-4x+2}}{x}=\frac{{2{{(x-1)}^2}}}{x}≥0$
∵f'(x)>0在定義域(0,+∞)內恒成立,
∴函數f(x)在(0,+∞)都是單調遞增.
(2)當a=4時,f(x)=x2-6x+4lnx,
則$f'(x)=\frac{{2{x^2}-6x+4}}{x}$,
∵x>0,
∴$f'(x)=2(x+\frac{2}{x}-3)≥4\sqrt{2}-6$.
∴曲線f(x)在定義域內的任意一點處的切線斜率都大于或等于$4\sqrt{2}-6$,
而$3∈[{4\sqrt{2}-6,+∞}]$,
∴曲線f(x)可以與3x-y+n=0中的一條直線相切,另一組直線無切線.
此時切線的斜率是3,對應的切線方程式y=3x-20+8ln2或$y=3x-\frac{17}{4}-4ln2$;
(3)由(2)得函數y=f(x)在點P(x0,f(x0))處的切線方程為
l:y=g(x)=$\frac{{2x}_{0}^{2}-6{x}_{0}+4}{{x}_{0}}$(x-x0)+x02-6x0+4lnx0.
若函數f(x)=x2-6x+4lnx存在“類對稱點”P(x0,f(x0)),
則等價與當0<x<x0時,f(x)<g(x),當x<x0時,f(x)>g(x)恒成立,
①當0<x<x0時,f(x)<g(x),恒成立,
等價于當0<x<x0時,${x^2}-6x+4lnx<\frac{{2{x^2}_0-6{x_0}+4}}{x_0}(x-{x_0})+{x^2}_0-6{x_0}+4ln{x_0}$恒成立,
即當0<x<x0時,${x_0}{x^2}-(2{x^2}_0+4)x+4{x_0}•lnx+{x^3}_0+4{x_0}-4{x_0}•ln{x_0}<0$恒成立.
令$ϕ(x)={x_0}{x^2}-(2{x^2}_0+4)x+4lnx•{x_0}+x_0^3+4{x_0}-4ln{x_0}•{x_0}$,
則ϕ(x0)=0,要使ϕ(x)<0在0<x<x0恒成立,只要ϕ(x)在(0,x0)單調遞增即可.
又∵$ϕ'(x)=2{x_0}x-(2{x^2}_0+4)+\frac{{4{x_0}}}{x}=\frac{{2(x{\;}_0x-2)(x-{x_0})}}{x}$,
∴${x_0}≤\frac{2}{x_0}$,即$0<{x_0}≤\sqrt{2}$.
②同理當x>x0時,f(x)>g(x)恒成立,${x_0}≥\sqrt{2}$,
∴${x_0}=\sqrt{2}$.
∴y=f(x)存在“類對稱點”,其中一個“類對稱點”的橫坐標是${x_0}=\sqrt{2}$.
點評 本題考查函數的單調區間的求法,考查類對稱點的求法.解題時要認真審題,注意挖掘題設中的隱含條件,合理地進行等價轉化,注意導數性質的靈活運用.


 沖刺100分1號卷系列答案
沖刺100分1號卷系列答案 期末好成績系列答案
期末好成績系列答案科目:高中數學 來源: 題型:解答題
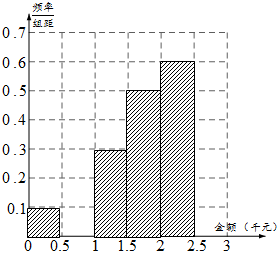 某網絡營銷部門為了統計某市網友“雙11”在某淘寶店的網購情況,隨機抽查了該市當天60名網友的網購金額情況,得到如下數據統計表(如圖):
某網絡營銷部門為了統計某市網友“雙11”在某淘寶店的網購情況,隨機抽查了該市當天60名網友的網購金額情況,得到如下數據統計表(如圖):| 網購金額 (單位千元) | 頻數 | 頻率 |
| (0,0.5] | 3 | 0.05 |
| (0.5,1] | x | p |
| (1,1.5] | 9 | 0.15 |
| (1.5,2] | 15 | 0.25 |
| (2,2.5] | 18 | 0.30 |
| (2.5,3] | y | q |
| 合計 | 60 | 1.00 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
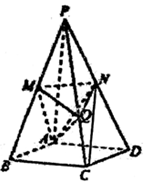 如圖,在四棱錐P-ABCD中,底面是邊長為2$\sqrt{3}$的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA=2$\sqrt{6}$,M、N分別為PB,PD的中點.
如圖,在四棱錐P-ABCD中,底面是邊長為2$\sqrt{3}$的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA=2$\sqrt{6}$,M、N分別為PB,PD的中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -$\frac{1}{4}$ | B. | $\frac{1}{4}$ | C. | -$\frac{1}{8}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com